Dany jest ostrosłup prawidłowy trójkątny EFGP, którego podstawą jest trójkąt EFG Robert: Dany jest ostrosłup prawidłowy trójkątny EFGP, którego podstawą jest trójkąt EFG. Kąt α nachylenia krawędzi bocznej EP do płaszczyzny podstawy ostrosłupa jest równa kątowi między krawędziami bocznymi EP i FP zawartymi w ścianie bocznej EPF tego ostrosłupa. Oblicz sinus kąta α. Obliczyłem sobie cos i teraz wystarczy z jedynki trygonometrycznej obliczyć sinusa. Czy dobrze rozumiem, że będzie tylko jedno (dodatnie) rozwiązanie sin²α, bo kąt jest mniejszy niż 90? Bo normalnie x²=√x v x²=−√x

Robert: nie zwracajcie uwagi na te "równania"

Eta:

	√1+2√7
sinα=
	3

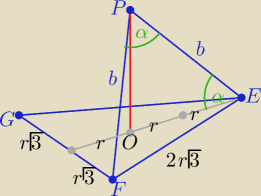
Eta: Najpierw poprawny rysunek Długość boku trójkąta EFG jest równa 2r√3 , gdzie r −− dł. promienia okręgu wpisanego w podstawę

	2r
W ΔOEP : cosα=
	b

	2b2−12r2
w ΔOEP z tw. kosinusów: cosα=
	2b2

porównując wartości cosinusów : otrzymujemy 4br=2b²−12r² /: 2 6r²+2br−b²=0 Δ_r=28b² √Δ=2√7b

	√7b−b		b
r=		=		(√7−1)
	6		6

to

	2r		√7−1		√1+2√7
cosα=		⇒ cosα=		to sinα=√1−cos2α =........ =
	b		3		3