trójkąt marcinek: W trójkącie równoramiennym ABC z wierzchołków A i B poprowadzono dwie wysokości ,które przecięły się w punkcie P. Wykaż ,że stosunek pól kół opisanych na trójkącie ABC i na trójkącie APB jest równy 1

Adamm: nie podałeś które boki są równe w trójkącie ABC

marcinek: |AC|=|BC|

Adamm: z tw. Sinusów

|AB|
	=2RAPB
sin∡APB

oraz

|AB|
	=2RACB
sin∡ACB

	RAPB		sin∡ACB		sin∡ACB
k=		=		=		=1
	RACB		sin∡APB		sin(180o−∡ACB)

koła te są podobne w skali k (dowolne dwa koła są podobne), a ich pola w skali

	PAPB
k2=		gdzie tutaj PAPB oraz PACB to pola odpowiednich kół
	PACB

	PAPB
skąd		=1 c. b. d. o.
	PACB

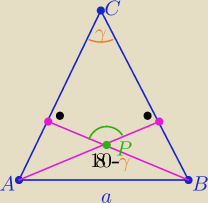
Eta: |<APB|= 180^o−γ to sin (180^o−γ)=sinγ Z tw. sinusów:

	a
dla ΔABC 2R1=
	sinγ

	a		a
dla ΔAPB 2R2=		=
	sin(180o−γ)		sinγ

długości promieni są równe ⇒ że i pola kół opisanych są równe zatem stosunek tych pól jest równy 1 c.n.w

Adamm: pierwszy

Eta:

Eta: Za to mój rysunek ładniejszy

Adamm: z tym niestety muszę się zgodzić