stereometria Kasia: Powierzchnia boczna stożka po rozwinięciu jest półkolem. Wynika stąd, że kąt rozwarcia stożka ma miarę x. Oblicz x

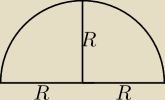
kochanus_niepospolitus: skoro mamy półkole ... to załóżmy, że tworząca = R

	R
obwód podstawy 2π		−> πR
	2

	R
czyli r =		−> 2r = R
	2

więc przekrój tego stożka (wierzhcołek + średnica podstawy) to trójkąt równoboczny o boku R. stąd kąt α ma miarę ...

Jerzy: l − tworzaca = promień rozwinięcia

1
	πl2 = πfl i r = lsinx (x = połowa kata rozwarcia )
2

1		1
	πl2 = πl2sinx ⇔ sinx =		⇔ x = 300
2		2

Kat rozwarcia = 2*x = 60^o

Kasia: 1 _πl2 = πfl i r = lsinx 2 nie rozumiem tego zapisu, co oznacza f?

Jerzy: Na Twoim rysunku R = l ( to zarazem tworzaca stożka )

	r
Na przekroju stozka mamy zależność:		= sinx ⇔ r = l*sinx
	l

Porównujemy pole przekroju i pole powierzchni bocznej stożka:

1
	π*l2 = π*r*l = π*l2*sinx
2