Wielomiany Donna: Zadanie maturalne: Wykaż, że dla każdej liczby rzeczywistej prawdziwa jest nierówność: x(x−1)(x−2)(x−3) +1≥0 doszłam do momentu, że: x⁴ − 6x³ + 11x² − 6x +1 ≥0 I próbuję to jakoś rozwiązać Hornerem, ale się nie da. Proszę o pomoc.

Adamm: podstawiając t=x−1,5 doprowadzisz równanie do prostszej postaci

Donna: Znaczy... Gdzie mam to "t" podstawić? I czemu akurat "x−1,5"?

Adamm: do równania, jasno się wyraziłem jeśli podstawisz t=x−1,5, wtedy x=t+1,5, x−1=t+0,5, x−2=t−0,5, x−3=t−1,5 wzory skróconego mnożenia sprawią że czynniki przy t³ oraz t się wyzerują

kochanus_niepospolitus: zauważ, że: x oraz x−3 są 'odległe' o '2' (a środek wypada w x−1.5) x−1 i x−2 są 'odległe' o '1' (a środek wypada w x−1.5) jeżeli zrobisz podstawienie: t = x − 1.5 ... czyli x = t + 1.5 to otrzymujesz: x = t + 1.5 x − 1 = t + 0.5 x − 2 = t − 0.5 x − 3 = t − 1.5 i masz: (t+1.5)(t+0.5)(t−0.5)(t−1.5) + 1 ≥ 0 i masz tutaj wzory skróconego mnożenia

Adamm: do nierówności

Donna: Dziękuję!

kochanus_niepospolitus: i otrzymujesz wtedy:

	9		1
(t2 −		)(t2 −		) ≥ −1
	4		4

i znowu podstawienie:

	5
w = t2 −
	4

i mamy: (w−1)(w+1) ≥ −1 w² − 1 ≥ −1 w² ≥ 0

kochanus_niepospolitus: więc: w² = (t² − 5/4)² = ((x−3/2)² − 5/4)² ≥ 0 dla dowolnego x∊R c.n.w.

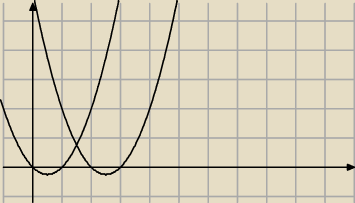
piotr: rozpatruj iloczyny wartości naksymalnych w odpowiednio małych przedziałach narysowanych funkcji albo po prostu pochodna

Donna: Próbowałam pochodną. Wyszło f'(x) = 4x³ −18x² +22x − 6 I nie mogłam znowu znaleźć miejsc zerowych, żeby obliczyć extrema funkcji...

kochanus_niepospolitus: Donna ... napisaliśmy Ci jak to zrobić możesz

drou: można obliczyć pochodną funkcji. z pochodnej odczytać minimum lokalne i podstawić minimum lokalne do wzoru funkcji. Ukazać że wartość funkcji dla mninimum lokalnego jest dodatnie

Donna: Tak, i podziękowałam. Ale nie ma na to jakiegoś prostszego sposobu? Jest to zadanie maturalne i gdybym na takie natrafiła za tydzień nie wpadłabym na to. Dlatego chcę dopytać jeszcze o inne sposoby...

Adamm: x=3/2 jest miejscem zerowym twojej pochodnej

kochanus_niepospolitus: 4x³ −18x² +22x − 6 = 0 chociażby dla x=3/2 (czyli magiczne masz x−1.5 )

drou: pochodna ma chyba 3 miejsca zerowe i 2 minimum lokalne

kochanus_niepospolitus: No ma ... ale mając jedno miejsce zerowe ... pozostałe już jest w stanie wyznaczyć (bo będzie miała wielomian kwadratowy).

StrasznyNieogar: Donna skąd masz takie zadanie?

Donna: Nowa Era − zbiór zadań maturalnych poziom rozszerzony

Donna: Teraz matura 2017. Matematyka Vademecum. Poziom rozszerzony

StrasznyNieogar: A okej. Mam nadzieje ze 9 maja takiego nie bedzie

Donna: Ja też.

drou: takie pytanko: jak wyznaczyliście x=3/2? 4x3 −18x2 +22x − 6 = 0

Adamm: 2x³−9x²+11x−3=0 tw. o pierwiastkach wymiernych licznik to dzielnik 3 a mianownik to dzielnik 2

jc: x(x−1)(x−2)(x−3) +1≥0 (x²−3x)* (x²−3x+2) + 1 ≥ 0 (x²−3x+1 − 1)(x²−3x+1 + 1) + 1 ≥ 0 (x²−3x+1)² − 1² + 1 ≥ 0 (x²−3x+1)² ≥ 0 komentarz... koniec dowodu [**]

Donna: jc Właśnie o coś takiego mi chodziło... Dziękuję ci bardzo!

kochanus_niepospolitus: ale i tutaj musisz 'coś' zauważyć ... jeżeli nie zauważyć, to 'pozamiatane'