Stereometria
Kasia: Jak będzie wyglądał przekrój sześcianku który przecięto płaszczyzną przechodzącą przez krawędź
dolnej podstawy i jeden z wierzchołków górnej podstawy? Proszę o rysunek
27 kwi 12:42
Jerzy:
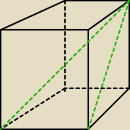
Mniej więcej tak.
27 kwi 12:46
Adamm: Jerzy, na pewno?
27 kwi 13:05
Kasia: Jak obliczyć objętości brył uzyskanych w wyniku tego przekroju jeżeli krawędź sześcianu wynosi
3?
27 kwi 13:08
Jerzy:
No pewnie , że nie

27 kwi 13:12
Adamm:
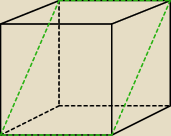
moim zdaniem płaszczyzna powinna wyglądać tak
27 kwi 13:13
Jerzy:
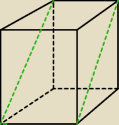
27 kwi 13:14
Jerzy:
Oczywiście

27 kwi 13:14
kochanus_niepospolitus:
zauważ, że bryła 'poniżej' przekroju to niż innego jak ostrosłup o tej samej podstawie co
sześcian i o tej samej wysokości.
| | 1 | |
więc: Vtego poniżej = |
| *3 = 1 |
| | 3 | |
więc: V
tego powyżej = 3 − 1 = 2
kooooniec

27 kwi 13:15
kochanus_niepospolitus:
Jerzy, Adam ... oczywiście że początkowo było dobrze
27 kwi 13:15
Jerzy:
Policz objetość graniastosłupa o podstawie trójkąta prostokatnego i wysokości h = 3
27 kwi 13:16
kochanus_niepospolitus:
| | 1 | |
tfu ... Vdolnego = |
| 33 = 9 ... Vgórnego = 18 |
| | 3 | |
27 kwi 13:17
Jerzy:
Nie... nie ma takiego przekroju jak narysowałem o 12:46
27 kwi 13:17
Kasia: | | 27 | |
W odpowiedziach mam podane, że objętość jednej z brył wynosi |
| |
| | 2 | |
27 kwi 13:17
Adamm: kochanus, jeśli to ostrosłup, o podstawie która ma 4 boki, to jak może mieć
3 ściany?
27 kwi 13:19
27 kwi 13:21
Jerzy:
Tak ma być , jak narysowaliśmy ja i Adamm
27 kwi 13:22
kochanus_niepospolitus:
Jerzy ... jak nie jak tak

Kurdę ... przez trzy punkty poprowadzisz płaszczyznę ... więc taki przekrój jak najbardziej
istnieje

27 kwi 13:26
kochanus_niepospolitus:
Dobra ... cofam co pisałem

27 kwi 13:28
Jerzy:
Nie masz racji

To co narysowałem, to jedynie trójkąt utworzony przez krawędż podstawy, przekatną ściany
i przekatną bryły

Takiego przekroju nie ma !
27 kwi 13:28
Adamm: przekrój istnieje, ale tak nie wygląda
odpowiednie odcinki sześcianu są równoległe, a skoro płaszczyzna przechodzi przez jeden z nich,
oraz punkt należący do naprzeciwległego to przechodzi przez oba
27 kwi 13:28
Jerzy:
Adamm ... teraz ja nie rozumiem...
Nie da się tak przekroić sześcian , aby otrzymać w przkroju trójkąt, który narysowałem.
27 kwi 13:32
 Mniej więcej tak.
Mniej więcej tak.

 moim zdaniem płaszczyzna powinna wyglądać tak
moim zdaniem płaszczyzna powinna wyglądać tak



 Kurdę ... przez trzy punkty poprowadzisz płaszczyznę ... więc taki przekrój jak najbardziej
istnieje
Kurdę ... przez trzy punkty poprowadzisz płaszczyznę ... więc taki przekrój jak najbardziej
istnieje 

 To co narysowałem, to jedynie trójkąt utworzony przez krawędż podstawy, przekatną ściany
i przekatną bryły
To co narysowałem, to jedynie trójkąt utworzony przez krawędż podstawy, przekatną ściany
i przekatną bryły  Takiego przekroju nie ma !
Takiego przekroju nie ma !