statystyka/prawdopodobienstwo kiniaswinia: Statystyka i prawdopodobieństwo pilne! 1. Przyjmijmy, że mamy szachownicę o polach, których krawędź ma długość a. Obliczyć prawdopodobieństwo, że rzucona moneta o promieniu r(r<a) przetnie co najwyżej jedną krawędź? 2. Pewne schronisko w górach ma tylko trzy pokoje: 4−osobowy, 3−osobowy i 2−osobowy. Nagle pojawia się w nim sześcioosobowa wycieczka i losowo zajmuje miejsca. Obliczyć prawdopodobieństwo, że jeden z pokoi pozostanie pusty.

kochanus_niepospolitus: 2)

	6*5*4*3*2*1
P(B) =
	9*8*7*6*5*4

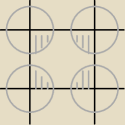
1) Patrz rysunek Aby moneta przecięła dwie krawędzie spadając na dane (konkretne) pole w szachownicy, środek monety musi upaść gdzieś w zaznaczonym obszarze (okręgi są o promieniu r). Stąd:

	πr2		a
P(A) = 1 −		o ile r <
	a2		2

	a
Jeżeli r >		to P(A) = 0
	2

Jerzy: 2) Tylko mianownik dobry

kochanus_niepospolitus: kuźwa ... no tak ... toć mogą 4'rkę i 3'jkę zająć

Jerzy: 1)

	6 4   6 3   2* +
P(A) =
	9*8*7*6*5*4

kochanus_niepospolitus: Jerzy ... jak na moje to winno być:

	6*5*4*3*2*1 + 7*6*5*4*3*2		8*6!
P(A) =		=
	9*8*7*6*5*4		9*8*7*6*5*4

Nie wiem czemu w liczniku korzystać z dwumianów Newtona

Jerzy: Mamy 3 możliwości: 1) Zajmują 4 i 3 ( 2 pusta )

	6 4
a) 4 osoby do 4 =		pozostałe 2 do 3

	6 3
b) 3 osoby do 4 =		pozostałe 3 do 3

2) Zajmują 4 i 2 ( 3 pusta )

	6 4
c) 4 osoby do 4 =		pozostałe do 2

Jerzy: Nie chce mi się tego liczyć, ale może mamy ten sam wynik ?

kochanus_niepospolitus: nie ten sam ... bo Ty w liczniku nie bierzesz pod uwagę kolejności, więc albo zmieniasz Ω albo pozbywasz się dwumianów nawet nie trzeba liczyć aby zobaczyć, że:

	6 4		6 3
2*		+		< 2*6! + 6! = 3*6! < 8*6!

Jerzy: Tak , u mnie trzeba by zmienić mianownik , więc pozostaję przy Twoim liczniku