stereometria Kasia: Podstawą graniastosłupa prostego ABCDEF jest trójkąt prostokątny ABC, a którym kąt CAB ma miarę 30, a przeciwprostokątna ma długość p. Przekątna ściany ACDF jest nachylona do przekątnej ściany BCDE pod kątem α. Oblicz wysokość graniastosłupa i wykaż że α<60

kochanus_niepospolitus: brakuje tutaj jakiejś danej

Kasia: Sprawdziłam, wszystkie dane podałam

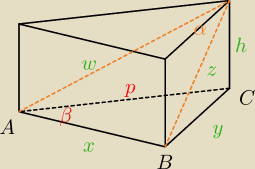
kochanus_niepospolitus: β = 30^o

	p
y = p*sin30o −> y =
	2

	p√3
x = p*cos30o −> x =
	2

w = √p²+h² z = √y²+h² = √p²/4 + h² z tw. cosinusów: x² = w² + z² − 2wzcosα

3		p2
	p2 = p2 + h2 +		+h2 − 2√p2+h2*√p2/4 + h2*cosα
4		4

	p2
2√p2+h2*√p2/4 + h2*cosα =		+ 2h2
	2

	p2
√p2+h2*√p2/4 + h2*cosα =		+ h2
	4

	p2		3p2
oznaczmy: a =		+ h2 −> a +		= p2 + h2
	4		4

zauważamy, że cosα > 0 √a+ 3p²/4*√acosα = a √(a² + 3ap²/4)cos²a = √a² (a² + 3ap²/4)cos²a = a²

3
	ap2cos2α = a2(1−cos2α)
4

3p2
	cos2α = asin2α
4

3p2		3p2		p2
	ctg2α = a −>		ctg2α =		+ h2
4		4		4

Z tego wynika, że:

	p2
h2 =		(3ctg2α − 1) <−−− masz wyznaczone 'h'
	4

3p2		p2
	ctg2α =		+ h2 ... wiemy, że h > 0, więc:
4		4

3p2		p2		1		√3
	ctg2α >		⇔ 3ctg2α > 1 ⇔ ctg2α >		⇔ ctgα >
4		4		3		3

czyli: α < 60^o (bo funkcja f(x) = ctgx jest funkcją malejącą)

Kasia: Dziękuję bardzo!