Wykaż, że objętość tego walca jest równa objętości kuli wpisanej w dany stożek. Matfiz: W stożek, którego przekrojem osiowym jest trójkąt równoboczny o boku 2a, wpisano walec o największej objętości. Wykaż, że objętość tego walca jest równa objętości kuli wpisanej w dany stożek. Proszę o pomoc

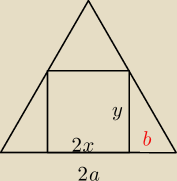
kochanus_niepospolitus: a więc po kolei: 1) V_walca = πx²*y

	y
2) tg60o =
	b

3) x+b = a x + b = a −> b = a−x

	y
tg60o =		−> √3b = y −> √3(a−x) = y
	b

V_walca = πx²*y = πx²(√3(a−x)) = √3πax² − √3πx³ V'_walca = ... i liczysz maksymalną objętość Później wystarczy pokazać jaka jest objętość kuli wpisanej w ten stożek (jako że przekrój to trójkąt równoboczny, to masz gotowe wzory)

Matfiz: Zrobiłem, ale coś mi dziwnego wyszło. Mógłbyś jeszcze może to dokończyć? Bo nie wiem w czym błąd zrobiłem

kochanus_niepospolitus: to pokaż jak robisz ... sprawdzę