geometria analityczna QQ: Rozwiąż układ równań y=|x−1| x²+y²−2x−4y+1=0 Jak rozwiązywać tego typu układy?

wmboczek: ogólnie metodą podstawienia i opuszczając || tu można zauważyć, że dolne równanie (x−1)²+y²−4y=0 oraz a²=|a|²

Jolanta: dolne rownanie to wzór okregu o środku w punkcie S(1,2) i promieniu r=2

QQ: może ktoś rozwiązać? bo chcę sprawdzić odpowiedzi

QQ: wyszło mi x=1 x=3 i x=−√2

QQ: :(

Jolanta: Dawno nie robilam tego typu zadań ,nie wiem jak dokładnie to zapisać y=|x−1| x−1≥0 x≥1 y=x−1 x−1<0 x<0 y=−x+1 x²+y²−2x−4y+1=0 x²+y²−2ax−2by+c=0 a=1 b=2 c=1 c=a²+b²−r² 1=1+4−r² r=2 y=−x+1 x²+x²−2x+12x+4(−x+1)+1=0 x²+x²−2x+1−2x−4x−4+1=0 2x²−8x−2=0 x²−4x−1=0 Δ=16+4=20 x₁=2−2√5 y₁=−2+2√5+1 i tak dalej

Jolanta: a juz widzę bląd mam +4 zamiast −

Jolanta: dla x <1 wychodzi x=−1 y=2 dla x≥1 x=1 y=0 x=3 y=2 możesz narysować i sprawdzic

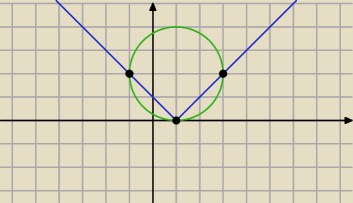
Jerzy: Trzy rozwiązania: (−1;2) (1;0) (3;2)

'Leszek: Rownanie drugie jest rownaniem okregu ( tak jak pokazal p.Jerzy) (x −1)² + (x −2)² = 4 I pierwsze rownanie ( nie mozna oposcic wartosci | | ) , mamy dwa przypadki 1) dla x ≥ 1 , y = x−1 i podstawiamy do rownania okregu 2) dla x< 1 , y = −x +1 i podstawiamy do rownania okregu Powodzenia !