Równania kwadratowe z wartością bezwzględną uczenn: Witam, Jak rozwiązywać tego typu równania: a) |x²−6|=2 b) |x²−4|+|x²−1|=4x+1 w b myślę że trzeba obliczyć w 5 przedziałach: 1(−nieskończoność,−2) 2(−2,−1) 3<−1,1) 4<1,2) 5<2,nieskończoność) ktoś wyjaśni?

SEKS INSTRUKTOR : Liczyć w przedziałach. Sprawdzić kiedy wartość bezwzględna się zeruje, przerzucić wszystko na jedną stronę i na przypadki.

Janek191: a) I x² − 6 I = 2 x² − 6 = − 2 lub x² − 6 = 2 x² = 4 lub x² = 8 x = − 2 lub x = 2 lub x = − 2√2 lub x = 2√2

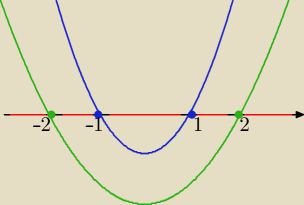
Eta: b) w przedziałach: 1/ x∊(−∞, −2> U <2,∞) 2/ x∊(−2,−1> U <1,2) 3/ x∊(−1,1)

g: Tego typu równania najlepiej jest rozwiązywać, korzystając z definicji wartości bezwzględnej. a)

	⎧	x2−6 gdy x2−6≥0
|x2−6| =	⎨		.
	⎩	−(x2−6) gdy x2−6<0

A więc x²−6=2 i x²−6≥0 x²=8 i (x−√6)(x+6p)≥0 x₁=√8, x₂=−√8 i x∊(−∞,−√6>∪<√6,∞). Oba rozwiązania należą do odpowiednich przedziałów, są więc rozwiązaniami tego równania.

g: Równanie dla dla x∊(−2√6, 2√6) ma postać: −(x²−6)=2 −x²+6=2 x²=4 x₃=2 , x₄ =−2. Oba rozwiązania należą do przedziału (−2√6, 2√6), są więc rozwiązaniami tego równania. Ostatecznie mamy cztery rozwiązania tego równania.

uczenn: (−∞,−2) U <2,∞) (x²−4)+(x²−1)= 4x+1 2x²−4x−6=0 Δ=64 x₁=(4−8)/4=−1 ∉ (−∞,−2) U <2,∞) x₂=3 ∊(−∞,−2) U <2,∞) (−2,−1> U <1,2) −(x²−4)+(x²−1)=4x+1 3=4x+1 x=1/2 ∉(−2,−1> U <1,2) x∊(−1,1) −(x²−4)−(x²−1)=4x+1 −2x²−4x+4=0 Δ=16+32=48 √Δ=4√3 x₁=(4−4√3)−4=−1+√3 x₂=−1−√3 ∉ (−1,1) odp x∊{−1+√3,3} Dobrze mniej więcej to zrobione? jeszcze takie pytanko, jak wyznaczać te przedziały?