funkcje iza:

	4x2
Wyznacz zbiór wartośći f(x)=
	x2 + x +2

Alky:

	32
ZW=<0,		>
	7

rafał: od czego zacząc ?

Alky: Cała ta funckja jest ciągła jako iloraz funkcji ciągłych, więc wystarczy, że znajdziesz minimum i maksimum.

Alky: Ew 2 sposób.

4x2
	=k
x2+x+2

Teraz sprawdzasz kiedy to ma rozwiązania, a więc 1) linowość 2) delta , ale 1 sposób chyba łatwiejszy. Ciężej się pomylić

Alky: Oczywiście w 2 sposobie trzeba wymoożyć mianownik, przerzucić wszystko na jedną stronę i dopiero liczyć 1) 2)

rafał: czyli policzyłam pochodna i co mam z nią dalej zrobic?>

Alky: "...więc wystarczy, że znajdziesz minimum i maksimum."

Mila: Zbiór wartości funkcji:

	4x2
f(x)=
	x2+x+2

x²+x+2>0 dla x∊R D=R

4x2
	=w
x2+x+2

4x²=wx²+wx+2w x²*(4−w)−wx−2w= 0 1) 4−w=0 ⇔w=4 wtedy mamy: −4x−8=0, x=−2 jedno rozwiązanie Lub 2) w≠4 mamy równanie kwadratowe, ma rozwiązania dla: Δ≥0 Δ=w²+8w*(4−w)=w²+32w−8w²=−7w²+32w −7w²+32w≥0 w*(−7w+32)≥0

	32
w=0 lub w=
	7

	32
w∊<0,		>=Zw
	7

Powracający: Rowniez skorzystam

rafał: policzylem pochodna i przyrównałem ją do 0 i otrzymałem x=0 i x = −4 i co dalej?

Alky: No i funkcja ma minimum w punkcie x=−4 i maksimum w x=0. f_min(−4)=0 f_max(0)={32}{7} . Funkcja jest ciągła więc f_min≤f(x)≤f_max

Mila: 1)

	32
fmax=f(−4)=
	7

f_min=f(0)=0 2) lim_x→∞f(x)=4 lim_x→−∞f(x)=4 asymptota pozioma

Alky: Oczywiście się pomyliłem. Powinno być na odwrót. f_min(0) i f_max(−4) , tak jak to Mila napisała

Mila: 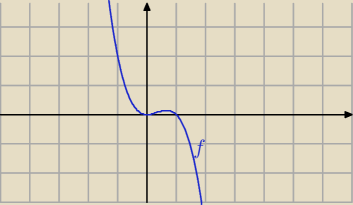Alky nie zawsze tak jest, jak piszesz 21:32 f(x)=x²−x³

Alky: Tak, rzeczywiście zapomniałem o tym. Trzeba oczywiście jeszcze policzyć granice. Dzięki Mila

Alky: I oczywiście niekoniecznie musi być tak jak pisałem 21:32, choć tu akurat nie chodziło mi o ten konkretny przypadek tylko generalnie. I może niekoniecznie dobrze się tam wyraziłem.

Mila: W tym zadaniu wszystko w porządku.

Alky: W tym tak. Śmieszne, że 20:56 zaproponowałem sposób którym robiłaś w 21:18 , ale powiedziałem, że może ten 1 łatwiejszy, bo ciężej o pomyłkę, a tymczasem gdyby zadanie było trochę inaczej sformułowane sam bym się tak pomylił

Mila: Tak to jest, uczymy się na błędach. TY takie zadania ładnie tu na forum rozwiązywałeś. Z pochodną to w niektórych przypadkach całe badanie funkcji.

Mila: Alky Nie robisz planimetrii i stereometrii?

Alky: Sporadycznie. Średnio lubię te zadania, więc o ile jest to możliwe staram się je omijać i jak już coś sobie robie dla przyjemności uciekając od "swojej" nauki np robiąc coś na forum to na pewno nie jest to planimetria ani tym bardziej stereometria. Nie to żebym był jakoś do nich zrażony albo uważał je jako najgorsze zło jak wiele osób, ale zniechęca mnie sposób rozwiązywania tych zadań. Kiedyś bardzo lubiłem te zadania, ale potem już trochę się nimi zmęczyłem i powiedzmy, że przestałem je robić. Teraz tylko jak w jakimś arkuszy się natknę to pomyślę i prędzej czy później zrobię natomiast generalnie nie lubię ich rozwiązywać

Adamm: ja wcześniej nie lubiłem planimetrii i stereometrii, ale niektóre zadania są dość ciekawe i dość przyjemnie się je rozwiązuje

Alky: Choć i z tym muszę w najbliższym czasie powalczyć, więc może nawet zaraz powalczę z czymś z planimetrii/stereometrii.

Powracający: czy Ty Alky piszesz mature teraz ?

Alky: Racja Adamm niektóre to nawet i mnie przypadają do gustu jak już się zabiorę. Oczywiście na moim poziomie O tyle ile zadania na liczenie jest w miare to dowody geometryczne mnie męczą. Co z tego, że na poziome maturalnym prawie zawsze znosi się to do twierdzenia cosinusów i czegoś jeszcze

Alky: @Powracający Tak

Jack: polecam nierownosci miedzy srednimi cauchy'ego, czasami sa w stanie pomoc na maturze, a nauczyc sie mozna w niecale 30min...

Adamm: ja polecam nierówność Schwarza oraz Jensena, a jak ktoś jest bardziej ambitny to również Holdera i Minkowskiego

Mila: Nie fiksujcie Panowie. To co jest w programie i otwarta głowa− to wystarczy.

Adamm: Jack zaczął, ja tylko dokończyłem

Alky: Też myślę, że jak na ten poziom to same nierówności pomiędzy 4 podstawowymi średnimi (pot,art,geo,harm) w zupełności wystarczą. Ostatnio jc pokazywał jakieś rozwiązanie przy użyciu wypukłości funckji i się trochę doedukowałem, ale ostatecznie myślę, że jak ktoś na poziomie maturalnym jest w stanie wpaść na rozwiązanie przy użyciu wypukłości czy nierówności które zaprezentowaliście, to tym bardziej może zrobić je używając prostszych metod ze szkoły średniej.

Adamm: Alky, dokładnie tak

Alky: Choć czasem warto co nieco się douczyć. Na przykład u mnie w szkole nie był w ogóle poruszany temat nierówności pomiędzy wyżej wymienionymi przeze mnie średnimi. Dopiero jakiś czas temu na forum zobaczyłem takie rozwiązanie i się poduczyłem, a teraz jak tylko widzę jakiś dowód algeraiczny to od razu myślę o tych średnich. Jeszcze Adamm pare dni temu sprostował nieco moją wiedzę na ten temat I dobrze, że się tego nauczyłem, bo badzo dużo dowodów maturalnych można robić przy ich użyciu

Adamm: Alky, mnie też tego nikt nie uczył mój wychowawca jedynie pewnego razu nie mógł poradzić sobie z zadaniem, i o nich wspomniał wtedy już wiedziałem mniej więcej co to pochodna, więc poradziłem sobie inaczej

Alky: U mnie w klasie ostatnio była taka sytuacja (niedawno zresztą, bo przyszedłem tego dnia ze względu na szkolenie maturzystów, a więc 2 dni temu<śmieszne swoją drogą, że maturzystów uczą przez 1,5 h, że jeśli chce się zaznaczyć odpowiedź to trzeba ją zamalować, natomiast w gimnazjum np nikt nie mówił co i jak odnośnie egzaminu gimnazjalnego, tylko mamy przyjść i napisać>), że mieliśmy do zrobienia jakiś dowód algebraiczny i jak zaproponowałem metodę nierówności między średnimi to wychowawczyni też tak nie do końca kojarzyła co i jak, musiała sobie przypomnieć. Dziwne, że jakoś się tego nie uczy. Według mnie to temat obowiązkowy jeśli chodzi o maturę z matematyki. Nie dość, że proste to jeszcze bardzo często moża to zastosować w dowodach.