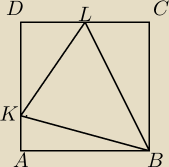
Na bokach AD i CD kwadratu ABCD o polu 1 wybrano punkty K i L w ten sposób, że k AdamBrzezinyPozdrawiam: Na bokach AD i CD kwadratu ABCD o polu 1 wybrano punkty K i L w ten sposób, że kąt KBL jest równy 45 stopni Oblicz odległość punktu K od prostej KL

AdamBrzezinyPozdrawiam: Punktu B od prostej KL*

Eta: https://matematykaszkolna.pl/forum/352375.html

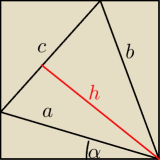g: poprzednią odpowiedzią trochę się wykpiłem, teraz na poważnie.

	1		1		√2
a =		; b =		=
	cos α		cos(45−α)		cos α+sin α

	1
c2 = a2+b2−2ab cos 45 = ..... =
	cos2α(cos α+sin α)2

	1		1
pole trójkąta =		ab sin 45 =
	2		2cos α(cos α+sin α)

	1		h
pole trójkata =		ch =
	2		2cos α(cos α+sin α)

h = 1

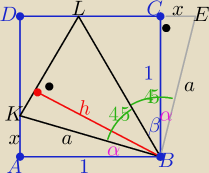Eta: 1/ odkładamy ΔBCE przystający do ΔABK to |∡LBE|=45^o bo α+45^o+β=90^o ⇒ β= 45^o−α Przystające są też trójkąty BKL i BLE z cechy (b,k,b) bo mają wspólny bok |BL| i |BK|=|BE|=a i kąt =45^o zatem h=|BC| = 1