Asyptoty pionowe i poziome wykresu funkcji Ferryda: Wyznacz asyptoty poziome i pionowe wykresu funkcji f

	x3 − 1
f(x)=
	x3 + x −2

asyptotę pionową obliczyłam, i sprawdziłam w odpowiedziach, dobrze. Ale rozwiązując wyszło mi też że jest asyptota pionowa w −1 (w odpowiedziach jej nie ma), i nie wiem czemu tak. Czy to dlatego , że granica przy x dążacym do 1 z prawej i lewej strony wyszła plus nieskonczoność ? Powinna być w jednym plus a w drugim minus ?

	1−16x2
f(x)=√
	4− x2

Jak ruszyć takie asyptoty z pierwiastkiem?

Adamm: dla x→−1 funkcja dąży do 1/2

Ferryda: Ale przecież, w mianowniku wychodzi 0+ albo 0− jak się podstawi minus jeden

Adamm: (−1)³+(−1)−2=−4

Ferryda: ups..pomyliłam znaki D: A jakby był taki przykład, że wyjdzie mi właśnie w lewostronnej i prawostronnej plus nieskończoność to wtedy jest to asyptota, tak? Nie musi w jednym wyjśc minus a w drugim plus nieskończoność

Adamm: nie musi

Adamm: może być tak że ±∞ wyjdzie tylko z jednej strony wtedy mamy asymptotę, ale tylko z tej jednej strony

Ferryda: Dziękuję, a czy pomógłbyś mi jeszcze z tą funkcją pod pierwiastkiem?

Adamm: x≠2, x≠−2

1−16x2
	≥0
4−x2

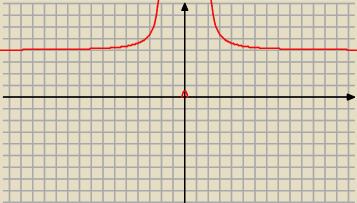
(x−1/4)(x+1/4)(x−2)(x+2)≥0 x∊(−∞;−2)∪<−1/4;1/4>∪(2;∞) liczysz granicę lim_x→−2⁻f(x), lim_x→2⁺f(x), lim_x→∞ f(x), lim_x→−∞f(x) i ukośne jak są tak to wygląda jak na rysunku, jakbyś chciał wiedzieć

Ferryda: A czemu w przedziałach jest (−niesk. , −2) i (2 , niesk.) ?, a nie tak jak z tymi 1/4? Bo nie wiem czy zrozumiałam to jak powinnam, bo tak jakby z każdego nawiasu podałam sobie warunek jaki musi zostać spełniony żeby ta liczba była większa od zera, x>1/4 i x>−1/4,,,,,ale tak teraz patrzę że to się kupy nie trzyma i tak i tak Nie pojmuję skąd wziąłeś przedziały do ,których nalezy x