Proszę o pomoc kokoriko: Promień okręgu opisanego na trójkącie prostokątnym jest równy R, a promień okręgu wpisanego w ten trójkąt wynosi r. Obwód tego trójkąta jest równy? Odpowiedź to 4R+2r. Ja tego nie widzę, pomóżcie

kokoriko: Pomożecie?

Ziemniak: Wychodzi

Ziemniak: spróbuję ci to narysowac ale nie znam się za bardzo na tej stronie

Ziemniak: http://2.bp.blogspot.com/-zfhHmJV61a8/U2uIjL0bGAI/AAAAAAAAFjY/_jeULLVRUiQ/s1600/Promien_okregu_wpisanego_i_opisanego_na_trojkacie_prostok%C4%85ntym_rownoramiennym_1.gif

Ziemniak: a−r=R wynika to z twierdzenie o odcinkach stycznej

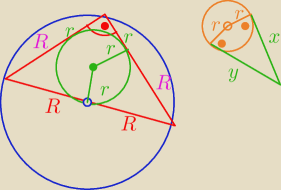
Jack: korzystamy jedynie z tej wlasnosci, ze jak mamy dwie proste (albo polproste) − w sensie wychodzace z tego samego wierzcholka i one sa styczne do danego okregu to odleglosci do punktu stycznosci sa sobie rowne tzn. patrz rysunek u gory po prawej (czyli x = y)

Adamm: Jack, dwa odcinki

Adamm: to się nazywa twierdzenie o odcinkach stycznych do okręgu

Jack: moga byc i odcinki...

kokoriko: Teraz to rozumiem, bardzo dziękuję wszystkim za pomoc

Eta:

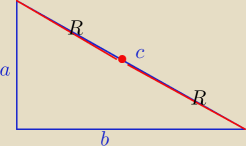
	a+b−c
r=		⇒ 2r=a+b−c i c=2R
	2

a+b=2r+c ⇒a+b=2r+2R to obwód L=a+b+c = 2r+4R