Trudne zadanko zef:

	6x2−72x+210
Na rysunku przedstawiono fragment funkcji f(x)=		określonej dla
	x2−12x+36

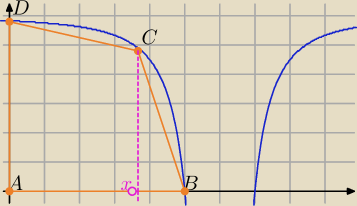
x∊(−∞;6). Wykres ten przecina osie Ox i Oy odpowiednio w punktach B i D, a punkt A jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty ABCD w których punkt C leży na wykresie funkcji y=f(x) pomiędzy punktami B i D. Oblicz pierwszą współrzędna wierzchołka C tego z rozpatrywanych czworokątów którego Pole jest największe. Wydaje się że łatwe zadanie. Wyznaczyłem współrzędne wszystkich punktów tj.: A(0,0), B(5,0)

	35
C(x0,f(x0)) D(0,		)
	6

Na raz tego pola nie policzę więc przedzieliłem wszystko na 2 pola (oddziela różowa linia przerywana) Powstają mi 2 pola, P1=Ax_oCD oraz P2=x₀BC Aby pole czworokąta było największe to suma tych pól również musi być największa P1+P2=P Zrobiłem porządek i wyszło mi

	−6x04+183x03−1548x02+3960x0
P=
	12x02−144x0+432

No i dalej jak zawsze pochodna itd. ale aż trudno sobie wyobrazić ile jest liczenia, przy pomocą geogebry jedynie udało mi się odczytać miejsca zerowe pochodnej i wyszło mi 4,18. Ma ktoś inny pomysł na to zadanie albo widzi błąd w moim rozumowaniu ?

Adamm: x²−12x+36=(x−6)² okazuje się że pochodna bardzo prosta do policzenia, szczególnie dlatego że reszta z dzielenia licznik przez mianownik jest stałą liczbą

zef: Mógłbyś dokończyć i zobaczyć ile wyjdzie ?

Adamm:

12
(x−6)3

Adamm:

	(5−x0)*f(x0)		x0*(35/6−f(x0))
P=		+x0*f(x0)+		=
	2		2

	35x0		5f(x0)
=		+
	12		2

	35		30
P'=		+
	12		(x0−6)3

przepraszam, nieprzytomny jestem

Adamm: zef? jesteś?

zef: Tak, tak jestem, widzę że podzieliłeś tą figurę na prostokąt i 2 trójkąty. Jeśli zauważyłbym że skróci się licznik z mianownikiem to na 2 dzieląc czworokąt na 2 pola też powinno wyjść