zb.wart przyszłymakler:

	1
1. jak udowodnić, że zbiór wartości funkcji f(x)= (		)|x| należy do (0;1)?
	2

2. określ dziedzinę i zbiór wartości funkcji f(x) = log_√2(8x−x²) <−−− w podstawie √2 D: x∊(0;8) f(x) = 2log₂x(8−x)

Jerzy: 1) Dla x ≥ 0 mamy: f(x) = (1/2)^x i Z_w = (0,1> Dla x < 0 mamy: f(x) = (1/2)^−x = 2^x i Z_w = (0;1)

Jerzy: 2) f(x) = log₂(8x − x²) gdy: x → 0 lub x → 0 , to f(x) → − ∞ f_max = f(4} = 2log₂16 = 8 Z_w = (−∞;8]

przyszłymakler: Odpowiedzią jest suma czy częśc wspólna? I nie da się tego jakoś bardziej rozpisać? Szczególnie dla x<0? Bo nie widzę tego szczerze mówiąc

Jerzy: f(x) = 2log₂(8x − x²) .... oczywiście.

przyszłymakler: 2) w pełni ogarniam, a cd. pierwszego Odpowiedzią jest suma czy częśc wspólna? I nie da się tego jakoś bardziej rozpisać? Szczególnie dla x<0? Bo nie widzę tego szczerze mówiąc

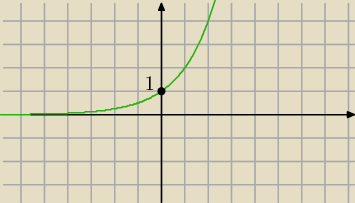
Jerzy: Suma. popatrz na rysunek i ustal jaki jest zbiór warości dla x < 0

przyszłymakler: Ok. Ja to wiem, tylko chciałęm wiedzieć, czy "takie rzeczy" się podaje bez większych dowodów czy właśnie tak bezpośrednio. Dziękuję za pomoc