Zadanko z prawdopodobienstwa z rownaniem
gielczunator: Ze zbioru X = {x ∊ C, |x−1| ≤ 4} losujemy dwa razy (ze zwracaniem) po jednej liczbie. Oznaczmy
te liczby w kolejności losowania a oraz b. Oblicz prawdopodobieństwo zdarzenia, że para liczb
(a,b) jest rozwiązaniem nierówności y−x+2 > 0, jeśli wiadomo że b jest nieujemna.
Prosiłbym o pomoc w tym zadaniu. Mój wynik to 24/81
Mój tok rozumowania:
I przypadek)
a − b + 2 > 0
a + 2 > b
więc a musi być o 1 mniejsze od b
Takich możliwości jest 8+7+...+2 tj. razem 30
II przypadek)
b −a + 2 > 0
b + 2 > a
więc b musi być o 1 mniejsze od a
Takich możliwości jest 5+4+..1 tj. razem 18
|Ω| = 9*9*2 (mnoże przez 2 bo kolejnośc czy x czy y)
P = 48 / 162 = 24 / 81
24 kwi 18:53
gielczunator: Czy na podst podanego polecenia powinienem załozyć, że a = x , b = y ?
24 kwi 18:54
Mila:
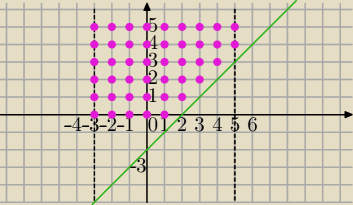
X={−3,−2,−1,0,1,2,3,4,5}
|Ω|=9
2=81
(a,b), a∊X, b∊{0,1,2,3,4,5} i b>a−2
|A|=44
24 kwi 21:37
 X={−3,−2,−1,0,1,2,3,4,5}
|Ω|=92=81
(a,b), a∊X, b∊{0,1,2,3,4,5} i b>a−2
|A|=44
X={−3,−2,−1,0,1,2,3,4,5}
|Ω|=92=81
(a,b), a∊X, b∊{0,1,2,3,4,5} i b>a−2
|A|=44