geometria analityczna Krakus: Punkty A = (2,4),B = (5,3) i C = (6,− 4) są sąsiednimi wierzchołkami czworokąta ABCD wpisanego w okrąg. Wierzchołek D tego czworokąta leży na prostej o równaniu y = 2x + 5 . Wyznacz współrzędne punktu D. Czy można to obliczyć stosując dwa razy twierdzenie cosinusów?

Krakus: Mam inny pomysł można obliczyć symetralne boków ab i bc i punkt przecięcia który będzie środkiem okręgu opisanego na tym czworokącie a potem podstawić współżędne punktu d do tego równania okręgu?

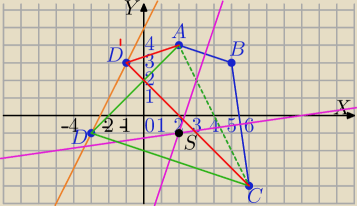
Mila: 1) symetralna AB: (x−2)²+(y−4)²=(x−5)²+(y−3)²⇔ y=3x−7 2) symetralna BC

	1		9
(x−5)2+(y−3)2=(x−6)2+(y+4)2⇔y=		x−
	7		7

3) punkt przecięcia S

	1		9
3x−7=		x−		, x=2
	7		7

S=(2,−1)⇒ R=|AS|=5 4) D(x, 2x+5) |DS|=5 (x−2)²+(2x+6)²=25 x=−3 lub x=−1 D=(−3,−1) lub D'=(−1,3)