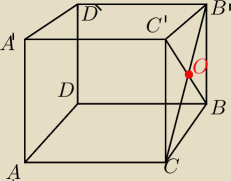
matma przyszłymakler: 1.W sześcianie punkt O jest punktem przecięcia przekątnych jednej ze ścian. Wykaż, że odcinek DO jest prostopadły do odcinka BC' Chciałem najpierw chciałem najpierw obliczyć odcinek DO z jakiegoś pitagorasa, lecz nie potrafię znaleźć rzutów prostokątnych, z tw. o 3 prostych z każdym odcinkiem, który próbuję obrać mam sprzeczność, mam problem z rzutami prostokątnymi punktów (ktoś ma może dobre materiały z objaśnieniem tego)? I ogólem zadania nie potrafię zrobić, także proszę o pomoc. 2. Tutaj WYMYŚLAM treść, bo gdzieś widziałem bardzo podobne zadanie i może ktoś z Was w swoim zbiorze ma je. To było coś takiego wielomian W(x) przy dzieleniu przez dwumian x−2 daje reszte 8, przy dzieleniu przez dwumian x−1 daje reszte 6, a przy dzieleniu przez dwumian x+2 daje resztę 3 wyznacz resztę z dzielenia wielomianu W(x) przez (x−2)(x−1)(x+2) nie potrzebuję rozwiązania, a jedynie schemat postępowania. Pozdrawiam.

'Leszek: W(x) = F(x)*(x−2)(x−1)(x+2) + R(x) R(x) = ax² + bx + c , reszta W(2) = 8 , W(1) = 6 , W(−2) = 3 R(2) = W(2) R(1) = W(1) R(−2) = W(−2)

przyszłymakler: Rozumiem, dziękuję! Pozostało jedynie nr. 1

Jerzy: Dobra treść zadania ? ( w przestrzeni proste prostopadłe muszą leżeć w jednej płaszczyźnie, a tutaj tak nie jest, one są skośne)

Jerzy: A sorry ..... przeczytałem prostopadły do B'C'

jc: Trójkąt CDB' jest równoramienny: DC=DB'. Dlatego DO jest wysokością trójkąta CDB'.

Jerzy: On jest nawet równoboczny.

'Leszek: Trojkat CDB ' jest rownoboczny , zas DO jest jego wysokoscia czyli DO prostopadly do CB ' , oraz CB ' prostapadla do BC ' i to konczy dowod

Jerzy: Prostopadłość CB' do BC' nie ma tu nic do rzeczy.

'Leszek: Wiem , przeciez wysokosc jest zawsze prostopodla do podstawy !

przyszłymakler: Genialne, a w dodatku takie oczywiste. Dziękuję Wam.