Wyznacz zbiór wartości k
bahama:
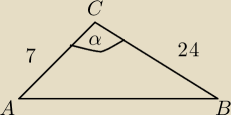
Wyznacz zbiór wszystkich wartości liczby k, dla których kąt α w trójkącie ABC nie jest ostry.
|AB| = k
3 − 7k + 25
Znalazłem już to zadanko na forum, jednak odpowiedź była niepełna. Prawidłowy zbiór to:
k∊<−
√7; −2>∪(−1; 0>∪<
√7; 3)
23 kwi 20:41
Eta:
Taki trójkąt spełnia warunek zadania gdy
1/ |AB|>0
i 2/ c<a+b
i 3/ jest prostokątny lub rozwartokątny gdy c
2≤ a
2+b
2
1/ k
3−7k+25>0 ⇒ ...........
2/ k
3−7k+25<24+7 ⇒ k
3−7k−6<0 ⇒ (k+1)(k+2)(k−3)<0 ⇒ k∊........
i 3/ (k
3−7k+25)
2≤625 ⇒ k
3−7k≤0 ⇒ ...........
Jako odp: podaj część wspólną tych trzech warunków
Otrzymasz taką odp jaką podajesz za poprawną

23 kwi 22:21
Kamila: A z pierwszego warunku jaki przedział wychodzi

10 sty 16:28
Mila:
Trudno będzie obliczyć bez wzorów np. Cardano. ( poczytaj)
Jeżeli jednak koniecznie chcesz mieć odpowiedź na pytanie (16:28), to tak.
Zatem f(k) =k
3−7k+25 ma jedno miejsce zerowe
Najmniejsza liczba z nierówności podanych przez
Etę to (−
√7)
f(−
√7)=−7
√7+7
√7+25>0
−3<−
√7
f(−3)=−27+21+25>0
−4<−3
f(−4)=−64+28+25<0
Wniosek:
k
0∊(−4,−3) więc spokojnie możesz napisać rozwiązanie wynikające z ( 2 ,3).
bo k
3−7k+25>0 dla k≥−
√7
16 sty 16:56
Mila:
| | 7 | |
Błąd w Δ ma być : (− |
| )3 |
| | 3 | |
16 sty 18:17
 Wyznacz zbiór wszystkich wartości liczby k, dla których kąt α w trójkącie ABC nie jest ostry.
|AB| = k3 − 7k + 25
Znalazłem już to zadanko na forum, jednak odpowiedź była niepełna. Prawidłowy zbiór to:
k∊<−√7; −2>∪(−1; 0>∪<√7; 3)
Wyznacz zbiór wszystkich wartości liczby k, dla których kąt α w trójkącie ABC nie jest ostry.
|AB| = k3 − 7k + 25
Znalazłem już to zadanko na forum, jednak odpowiedź była niepełna. Prawidłowy zbiór to:
k∊<−√7; −2>∪(−1; 0>∪<√7; 3)

