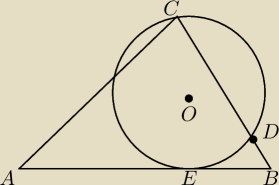
 W trójkącie ABC mamy dane IABI= 14, IBCI=9, I∡CBAI=60o. Punkt D leży na boku BC i ICDI=8.
Przez punkty C i D poprowadzono okrąg, który jest styczny do odcinka AB. Oblicz promień tego
okręgu.
W trójkącie ABC mamy dane IABI= 14, IBCI=9, I∡CBAI=60o. Punkt D leży na boku BC i ICDI=8.
Przez punkty C i D poprowadzono okrąg, który jest styczny do odcinka AB. Oblicz promień tego
okręgu.
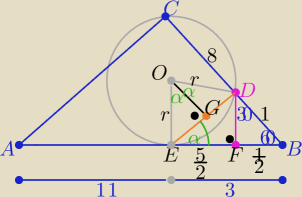 1/ z tw. o stycznej i siecznej |EB|2=|BC|*|BD| ⇒ |EB|2=9 ⇒ |EB|=3
2/ z własności trójkąta "ekierki" FBD
1/ z tw. o stycznej i siecznej |EB|2=|BC|*|BD| ⇒ |EB|2=9 ⇒ |EB|=3
2/ z własności trójkąta "ekierki" FBD
| 1 | √3 | |||
|FB|= | i |FD|= | |||
| 2 | 2 |
| |EG| | ||
trójkąt EOD równoramienny o ramionach "r" to r= | ||
| sinα |
| √3 | ||
|ED|=√(5/2)2+(√3/2)2= √7 to |EG|=√7/2 i sinα= | ||
| 2√7 |
| |EG| | 7√3 | |||
zatem r= | =................ r = | |||
| sinα | 3 |

 Coś nie tak?
Coś nie tak?
