ostrosłup klak: Matura Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość a; wysokość ściany bocznej wynosi 2a. Oblicz pole przekroju ostrosłupa płaszczyzną zawierającą krawędź podstawy i przechodzącą przez środki przeciwległych krawędzi bocznych.

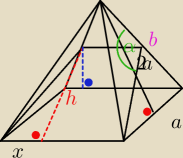
Adamm: taki przekrój jest oczywiście trapezem

	1
z podobieństwa trójkątów krótsza podstawa trapezu wynosi		a
	2

	3
P=		a*h
	4

	1   a− a   2		a
x=		=
	2		4

teraz niech d to środkowa (brakuje mi miejsca na rysunku) z tw. Pitagorasa b=√17a/2 z tw. Cosinusów

	1
(		b)2+d2−bdcosα=b2
	2

	1
(		b)2+d2+bdcosα=a2
	2

d²=b²/4+a²/2 d²=25a²/4 d=5a/2 z tw. Pitagorasa h=√d²−x²=3√11a/4 P=9√11a²/16

klak: ja mam zupełnie inną odpowiedz

Adamm: jakbyś powiedział jaką, byłoby fajnie

Adamm: pomyliłem się przy liczeniu środkowej d²=25a²/16 d=5a/4 h=√d²−x²=√6a/2 P=3√6a²/8 taka jest odpowiedź?

klak: 3a²√6/8 Może bład w odpwiedzi

klak: teraz jest ok dzięki