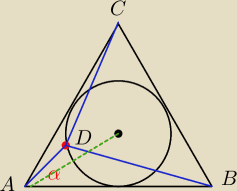
|AD|=a, |BD|=b, |CD|=c
założymy że D nie leży na bokach trójkąta (sprawdź sobie sam)
dodatkowo założymy że α>30o (możemy tak założyć)
z tw. Cosinusów
a2+1−2acosα=b2
a2+1−2acos(60o−α)=c2
a2+b2+c2=3a2+2−2√3acos(α−30o)
ponownie z tw. Cosinusów
| 2 | 2 | |||
( | h)2+a2−2a( | h)*cos(α−30o)=r2 | ||
| 3 | 3 |
| √3 | ||
P= | oraz P=p*r gdzie p to pół obwodu skąd | |
| 4 |
| √3 | ||
r= | ||
| 6 |
| 2 | √3 | ||
h= | |||
| 3 | 3 |
| √3+4√3a2 | ||
cos(α−30o)= | ||
| 8a |