Trójkąt rozwartokatny kappa: W trójkącie ABC mamy dane: |AC| = 12, |BC| = 16 oraz |∠ACB| = 120°. Przez wierzchołek C poprowadzono prostą prostopadłą do boku AC. Przecięła ona bok AB w punkcie D. Oblicz: a) długość odcinka CD b) promień okręgu opisanego na trójkącie ABC

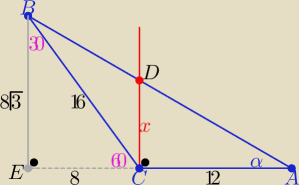
Eta: 1/ oznaczenia jak na rys. 2/ z tw. Talesa

	8√3		20
		=		⇒ .... x=|CD|=4,8√3
	x		12

3/ z tw. Pitagorasa w ΔBEA: |AB|²=(8√3)²+20² ⇒ |AB|=4√37

	8√3		2√3
4/ sinα=		=
	4√37		√37

	16
5/ z tw. sinusów wΔABC : 2R=		⇒ R=......................
	sinα