Pochodna
Powracający: Obliczam pochodna funkcji y=x
x
logarytmuje stronami
lny= lnx
x
lny=x*lnx
Rozniczkuje stronami
| 1 | | 1 | |
| y'= 1*lnx+x* |
| = lnx+1 |
| y | | x | |
Pytanie .
Dlaczego taka lewa strona tego rownania ?
22 kwi 21:38
Adamm: pochodna logarytmu+ pochodna funkcji złożonej
22 kwi 21:39
Powracający: | | 1 | |
Wlasnie tego nie rozumiem bo pochodna lny= |
| wiec skad jeszcze y'? |
| | y | |
22 kwi 21:41
Adamm: pochodna funkcji złożonej
nie liczysz pochodnej po y, tylko po x
sama pochodna logarytmu ci nie wystarczy
22 kwi 21:43
Adamm: przykład, mam nadzieję że dobry
niech y=x
2
ale jeśli chcielibyśmy policzyć po y to mielibyśmy (czyli tak jak ty)
duża różnica
22 kwi 21:50
Powracający: Chyba łapie
Czyli dalej mam
y'= (lnx+1)*x
x
22 kwi 21:52
Powracający: nastepne cwiczenie
xx mozna zapisac w postaci exlnx
Skorzystaj z tej postaci i oblicz pochodna funkcji xx poslugujac sie odpowiednimi wzorami
22 kwi 22:59
Adamm: wzór na pochodną funkcji złożonej
(exlnx)'=exlnx*(xlnx)'
22 kwi 23:00
22 kwi 23:01
Powracający: dzieki Adamm
A wtylumaczysz dleczego mozemy zapisac xx jako e{xlnx?
22 kwi 23:03
Adamm: ze wzoru alogab=b
zachodzi on prosto z definicji logarytmu
oczywiście trzeba założyć x>0
22 kwi 23:08
Adamm: ale dla x<0 i tak pochodna by nie istniała, bo funkcja nie jest ciągła dla x<0
22 kwi 23:08
Adamm: no chyba że dochodzą liczby zespolone
22 kwi 23:09
Powracający: Dobrze . dzieki .
Do zespolonych daleka droga u mnie
22 kwi 23:14
Powracający: czyli (xx)'= exlnx*( lnx+1)
22 kwi 23:21
Adamm: policzyłeś to niedawno

22 kwi 23:22
Powracający:
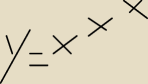
Dalej
Oblicz pochodna funkcji (na rysunku )
Wskazowka Zasatosuj jeden raz metode pochodnej logaryrtmicznej podstawiajac za pochodna
funkcji u=x
x jej wartosc obliczona w poscie 21 : 52
23 kwi 10:14
Powracający: Mozemy to zapisac tak
y= u
x gdzie u=x
x
(lny)'= (lnu
x)'
23 kwi 10:36
Powracający: dalej
y'= (x*lnxx)'*xxx
y'= [lnxx+x*(ln+1)*xx]*xxx
czy dobrze jest i czy dobrze postawilem ten nawias kwadratowy ?
23 kwi 11:19
Powracający:
23 kwi 12:31
Adamm: tam przy logarytmie nie masz argumentu
jak chcesz pisać xxx bardziej złożone potęgi to weź całą potęgę w klamerki { }
23 kwi 12:36
Powracający: dzieki czyli jest dobrze .
23 kwi 12:40
Adamm: nie do końca
tam w tym nawiasie jeszcze xx nie powinno być
23 kwi 12:42
Powracający: Dlaczego ?
23 kwi 12:44
Adamm: po prostu
(xlnxx)'=lnxx+x*(xlnx)'=lnxx+x(lnx+1)
23 kwi 12:46
Powracający: Dobrze .
23 kwi 12:48
Powracający: I ostatnia kwestia zwiazana z tym
Uzasadnij ze jezeli u(x) i v(x) sa funkcjami x przy czym u(x)>0 to
(uv)'= v*uv−1*u'+uv*lnu*v'
23 kwi 17:47
Adamm: u=elnu
i znowu wzór na pochodną złożoną + pochodna iloczynu
23 kwi 17:48
Powracający: Nie bardzo to rozumiem . Dlaczego u=elnu ?
23 kwi 17:53
Adamm: z definicji logarytmu
logab to taka liczba że jeśli podniesiemy a do jej potęgi to otrzymamy b
23 kwi 17:57
Powracający: Musze to dobrze przemyslec
23 kwi 17:59

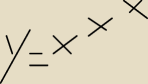 Dalej
Oblicz pochodna funkcji (na rysunku )
Wskazowka Zasatosuj jeden raz metode pochodnej logaryrtmicznej podstawiajac za pochodna
funkcji u=xx jej wartosc obliczona w poscie 21 : 52
Dalej
Oblicz pochodna funkcji (na rysunku )
Wskazowka Zasatosuj jeden raz metode pochodnej logaryrtmicznej podstawiajac za pochodna
funkcji u=xx jej wartosc obliczona w poscie 21 : 52