Trójkąt równoramienny
kset: Dany jest trójkąt równoramienny ABC, gdzie |AC| = |BC| = 4√3. Wysokośc opuszczona na
podstawę trójkąta jest równa odcinkowi łączącemu środek podstawy ze środkiem ramienia.
Oblicz różnicę między długością promienia okręgu opisanego na trójkącie ABC a długością
promienia okręgu wpisanego w dany trójkąt ABC. Do okręgu wpisanego w trójkąt ABC
poprowadzono styczną równoległa do podstawy, przecinającą ramiona trójkąta w punktach M i N.
Znajdź długość odcinka MN.
22 kwi 18:48
Eta:
|MN|=6(11−6
√3)
Czy taką masz odpowiedź ?
22 kwi 19:14
Adamm:
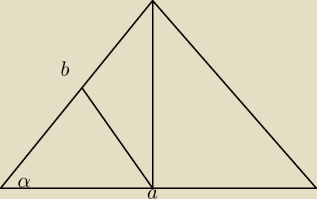
z tw. Sinusów mamy
h=2
√3 (sin2α=2sinαcosα, sinα=h/4
√3)
a=2*
√(4√3)2−(2√3)2=12
P=r*(a+b+c)/2 ⇒ r=12−6
√3
R−r=18
√3−12
22 kwi 19:16
22 kwi 19:18
Adamm: no tak

22 kwi 19:20
Eta:
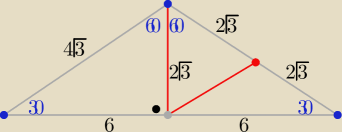
22 kwi 19:20
Eta:
R−r=.......
i licz maturzysto..........................
22 kwi 19:23
Eta:
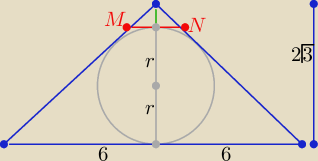
|MN|=x
z podobieństwa trójkątów
| 12 | | 2√3 | |
| = |
| ⇒ x=................. |
| x | | 2√3−2r | |
i dokończ obliczenia .................
22 kwi 19:29
 z tw. Sinusów mamy
z tw. Sinusów mamy


 |MN|=x
z podobieństwa trójkątów
|MN|=x
z podobieństwa trójkątów