równanie kamil852: wyznacz wszystkie wartości m dla których równanie cos²x−cosx+2=0 ma co najmniej jedno rozwiązanie ułożyłem równanie z parametrem t. podstawiłem do założenia, że Δ≥0 wyszedł mi przedział <1/4,∞) co dalej?

Mila: Nie widzę parametru m w równaniu.

kamil852: zamiast liczby '2' parametr m, mój błąd, wybacz

Adamm: z tą deltą to coś źle

Adamm: m∊<0;1/4>

kamil852: w odpowiedzi jest <−2,1/4>

Adamm: boże, weź, pomyliłem się

kamil852: nie wiem tylko skąd ta '2'

Adamm: f(x)=cos²x−cosx zacznij od zbioru wartości

Adamm: cos²x−cosx=−m −m musi należeć do zbioru wartości funkcji f(x)

kamil852: rozpisałbyś mi to? bo nie wiem czy dobrze liczę

Adamm: f^*(t)=t²−t, t∊<−1;1> f(1)=0, f(−1)=2, f(1/2)=−1/4 −1/4≤−m≤2

Adamm: tam powinny być f^* zamiast f przy liczeniu wartości dla 1, −1, 1/2

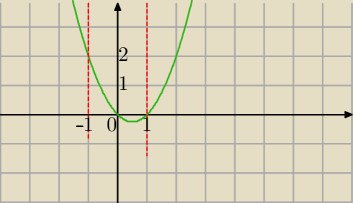
Mila: I sposób 1) cos²x−cosx+m=0 cosx=t, |t|≤1 t²−t=−m f(t)=t²−t 2) zbiór wartości f(t)

	1
tw=−
	2

	1
f(t)=−		najmniejsza wartość f(t)
	4

f(1)=0 f(−1)=2 największa wartość f(t)

	1
−		≤−m≤2 /*(−1)
	4

	1
−2≤m≤
	4