trygonometria
cotyniepowiesz98: Znajdź największe rozwiązanie równania w przedziale (0,2pi)
cos 2x − cos(2x+pi/2)=1
ja zrobiłam tak:
cos 2x − (cos2xcos pi/2 − sin2xsin pi/2)=1
cos2x + sin 2x = 1
1−sin2x + sinxcosx=1
sinx (cosx − sinx) = 0
sinx = 0 lub cosx=sinx
w przedziale wyszły rozwiązania: x=pi, x=pi/4, x=5pi/4
więc największe wychodzi x=5pi/4
a w odp jest pi/4... gdzie mam błąd?
22 kwi 17:25
Janek191:
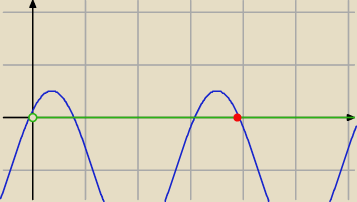
22 kwi 17:29
cotyniepowiesz98: nie bardzo rozumiem...?
22 kwi 17:32
Janek191:
Czerwony punkt.
22 kwi 17:34
cotyniepowiesz98: No dobrze, ale jak to się ma do mojego pytania?
22 kwi 17:35
Janek191:

22 kwi 17:37
cotyniepowiesz98: Naprawdę nie mogę zrozumieć co masz na myśli...
22 kwi 17:40
Janek191:
| | 5 | |
Z wykresu wynika,że największym rozwiązaniem w podanym przedziale jest liczba |
| π. |
| | 4 | |
22 kwi 17:42
cotyniepowiesz98: No ale właśnie w odp. podane jest, że powinno wyjść pi/4...
22 kwi 17:43
Janek191:
cos 2 x + sin 2 x = 1
2 cos
2 x − 1 + 2 sin x*cos x = 1 / : 2
cos
2 x + sin x*cos x = sin
2 x + cos
2 x
sin
2 x − sin x*cos x = 0
sin x*(sin x − cos x) = 0
sin x = 0 lub sinx = cos x
| | π | | 5 | |
x = π lub x = |
| lub x = |
| π |
| | 4 | | 4 | |
22 kwi 17:51
Janek191:
| π | |
| to najmniejsze rozwiązanie. |
| 4 | |
22 kwi 17:53
cotyniepowiesz98: to widocznie autorzy podręcznika się pomylili...
22 kwi 17:55
Janek191:
Tak mi się wydaje

22 kwi 18:01


