parametr funkcja kwadratowa StrasznyNieogar: Wyznacz te wartości parametru k , dla których równanie 2 (k + 1)x − 2x + k − 1 = 0 ma dwa różne rozwiązania należące do przedziału (0;2) funkcja musi być kwadratowa k nie może być − 1 Δ > 0 ===> k∊ ( − √2; √2 ) Teraz co? Widzialem gdzieś ze trzeba wyznaczyć, by wierzcholek był w podanym przedziale. Za bardzo tego nie rozumiem czemu, nie wystarczy wyznaczyć same miejsca zerowe? Wytłumaczy ktoś jak to zrobić? Za bardzo nie rozumiem

Janek191: Tam nie ma funkcji kwadratowej

Adamm: kwadratowa czy liniowa?

StrasznyNieogar: A no sorry (k + 1)x² − 2x + k − 1 = 0

Adamm: wystarczy wyznaczyć same miejsca zerowe, ale tak będziesz się tylko męczył wierzchołek w tym przedziale to nie jedyny warunek f(0)*(k+1)>0 oraz f(2)*(k+1)<0

Adamm: f(0)*(k+1)>0 oraz f(2)*(k+1)>0

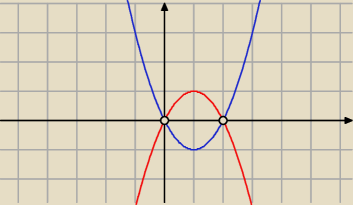
Janek191: p = 1

Monia: Nie koniecznie musi być wierzchołek p = 1 wydaje mi się

Adamm: ale może

Janek191: Niekoniecznie

StrasznyNieogar: Jeśli | x1| = |x2 − 2| wtedy p=1? W sumie nieważne f(0)*(k+1)>0 oraz f(2)*(k+1)<0 Nie bardzo rozumiem jakbyś wytłumaczył

StrasznyNieogar: f(0) > 0 wystarczy to?

StrasznyNieogar: I tak samo f(0) < 2

Adamm: no więc tak, na spokojnie zamiast paraboli pomyślmy o przedziałach (−∞;x_w> oraz <x_w;∞) w tych przedziałach funkcja odpowiednio rośnie i maleje (niekoniecznie w tej kolejności) z warunku delty wiemy że funkcja przecina oś OX w dwóch miejscach wiemy że funkcja rosnąca lub malejąca może przecinać oś OX jedynie w jedynym miejscu zatem w każdym z przedziałów mamy jedno miejsce zerowe (ale nie w punkcie x_w) zatem istnieje jakiś x₁∊(−∞;x_w) oraz jakiś x₂∊(x_w;∞) jeśli x_w≤0 w takim razie x₁<0, podobnie jeśli x_w≥2 to x₂>2 i nie choć jedno z miejsc nie zawiera się w przedziale, dlatego zakładamy że 0<x_w<2 kolejno, monotoniczność zależy od współczynnika przy największej potędze, czyli k+1 dla uproszczenia przyjmiemy k+1>0, zatem dla pierwszego przedziału funkcja maleje, dla drugiego rośnie w pierwszym przedziale jeśli f(0)>0 to ponieważ funkcja maleje, wiemy że x₁ znajduje się między x₁ a x_w (x₁<x_w z założenia) co jest wystarczające podobnie dla drugiego przedziału jeśli f(0)≤0 to ponieważ funkcja maleje, wiemy że x₁ znajduje się za 0, więc pierwiastek nie znajduje się miedzy 0 a 2, i podobnie dla drugiego zatem warunkami wystarczającymi oraz koniecznymi są podane wyżej

StrasznyNieogar: Muszę się chyba z tym przespać

StrasznyNieogar: Dzięki