Geometria analityczna Znawca: Dane są współrzędne wierzchołków A(−3,−2) i C(2,8) trapezu ABCD. Oblicz współrzędne punktu przecięcia przekątnych tego trapezu, jeżeli podstawa AB jest cztery razy dłuższa od podstawy DC. oznaczyłem sobie tak: A(−3,−2) B(x_B,y_B) C(2,8) D(x_D,y_D) punkt przecięcia przekątnych S(x_s,y_s) Wyliczyłem wektor →AC=[5,10] Potrzebuję jakiejś wskazówki co dalej.

Tadeusz: Zrób rysunek Z podobieństwa trójkątów wynika jak punkt przecięcia przekątnych dzieli AC

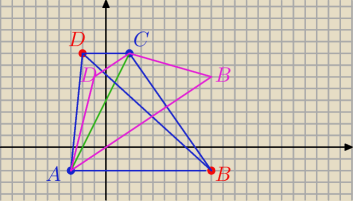
Janek191: Nie za mało danych ?

Znawca: Rysunek miałem zrobiony . OK, czyli skala będzie k=1/4, podzielę odcinek |AC| na 4 części, więc odcinek |SC|=1/4|AC|, a odcinek |AS|=3/4|AC|. Zaraz dokończę i w razie czego napiszę. Dziękuję za pomoc.

Tadeusz: ... tylko zastanów się na ile części

Znawca: na pięć jednak

Tadeusz:

Znawca: Git, wszystko się zgadza. S(1,6) wychodzi. Dziękuję jeszcze raz.

Janek191: → →

	4
AS =		AC
	5

	4
[ x + 3, y + 2] =		[ 5, 10]
	5

[ x + 3, y + 2 ] = [ 4, 8 ] x + 3 = 4 y + 2 = 8 x = 1 y = 6 S = ( 1, 6) ==========

Znawca: no tak, przecież wektorami też można to zrobić i to nawet szybciej wychodzi, bo ja teraz liczyłem odległości między punktami. Ale i tak najważniejsze żeby dobrze było. Dzięki.

Tadeusz: