 Student w czasie egzaminu odpowiada na 3 pytania. Aby zdać egzamin musi udzielić poprawnej
odpowiedzi na conajmniej 2 pytania. Prawdopodobieństwo, że odpowiedź na pojedyncze pytanie
jest poprawna wynosi 0,8. Oblicz prawdopodobieństwo tego, że student zda egzamin.
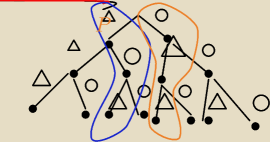
Robiłem sobie to drzewkiem:
I teraz
Trójkąt odznacza prawidłową odpowiedź.
Okrąg błędną.
Prawidłowa odpowiedź to 0,8
Błędna 0,2
I teraz
Prawdopodobieństwo, że student odpowie na 3 pytania dobrze wynosi:
Student w czasie egzaminu odpowiada na 3 pytania. Aby zdać egzamin musi udzielić poprawnej
odpowiedzi na conajmniej 2 pytania. Prawdopodobieństwo, że odpowiedź na pojedyncze pytanie
jest poprawna wynosi 0,8. Oblicz prawdopodobieństwo tego, że student zda egzamin.
Robiłem sobie to drzewkiem:
I teraz
Trójkąt odznacza prawidłową odpowiedź.
Okrąg błędną.
Prawidłowa odpowiedź to 0,8
Błędna 0,2
I teraz
Prawdopodobieństwo, że student odpowie na 3 pytania dobrze wynosi:
| 8 | 8 | 8 | |||
* | * | = 0,512 | |||
| 10 | 10 | 10 |
| 8 | 8 | 2 | |||
* | * | = 0,128 | |||
| 10 | 10 | 10 |
 Drzewko
A− poprawna odpowiedź
A' − błędna odp.
Z− student zdał
P(Z)=0.83+0.8*0.8*0.2+0.8*0.2*0.8+0.2*0.8*0.8=0.896
Drzewko
A− poprawna odpowiedź
A' − błędna odp.
Z− student zdał
P(Z)=0.83+0.8*0.8*0.2+0.8*0.2*0.8+0.2*0.8*0.8=0.896