,.,.,., Pełcio: Dobry wieczór. Jeszcze dziś... 1. Wykaż, że nie istnieją liczby wymierne dodatnie a,b,c,d spełniające równość: (a+b√2)⁴+ (c+d√2)⁴= 4+√5 2. Dowieść, że dla każdego trójkąta zachodzą nierówności:

1		1		1		1
	<		+		<		, gdzie r− promień koła wpisanego w ten trójkąt, zaś
2r		h1		h2		r

h₁.h₂ są wysokościami tego trójkąta. 3. Znajdź zbiór wszystkich środków okręgów zewnętrznie stycznych do okręgu x²+y²= 4 i jednocześnie stycznych do prostej o równaniu y=−2. 4. Rozwiąż równanie: x²−[x]=2

Saizou : ZADANIE 2 proponuję rozpatrzeć równoważną nierówność, poprzez podstawienie

	1		2P		2P
P=		ah1→h1=		oraz h2=
	2		a		b

	a+b+c		2P
P=		r→r=
	2		a+b+c

Adamm: 4. x²−x≤x²−[x]<x²−x+1 x²−x−2≤0 ∧ 0<x²−x−1

1+√5		1−√5
	<x≤2 ∧ −1≤x<
2		2

	1+√5
1.		<x≤2
	2

wiemy że x=√q gdzie q jest całkowite zatem q=3 lub q=4 x=√3 lub x=2, oba spełniają równanie

	1−√5
2. −1≤x<
	2

x=−√q gdzie q jest całkowite zatem q=1 x=−1 również spełnia równanie odp. x∊{−1; √3; 2}

Adamm: skąd wiemy że x=±√q gdzie q jest całkowite? ponieważ z równania x² jest całkowite, więc musi być pierwiastkiem liczby całkowitej

Adamm: tam zamiast koniunkcji miała być alternatywa

Pełcio: Saizou właśnie kombinowałem z tymi 2 wzorami, ale trochę inaczej to robiłem. Za chwilkę spróbuję, dzięki Za 4 też dzięki Adamm, robiłem z cechą może z 1 zadanie, średnio mi to idzie póki co.

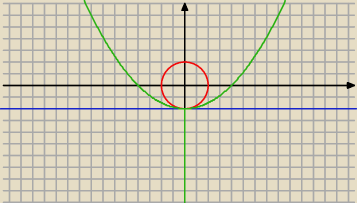
Adamm: S=(x; y), odległość S do y=−2 musi wynosić r oraz odległość S od (0; 0) musi wynosić r+2 d=|y+2|=r |OS|=√x²+y²=r+2 √x²+y²=|y+2|+2 dla y≥−2 x²+y²=y²+8y+16

	x2−16
y=
	8

dla y≤−2 x=0

Adamm: oczywiście nie podałem dziedziny, ale y≠−2

Pełcio: hm, 3 linijka to co to jest?

Adamm: d? odległość prostej od środka okręgu

Pełcio: miejmy nadzieję, że takiego zadania nie będzie ale dlaczego to d jest wprowadzone?

Adamm: zawsze tak oznaczam to jest zadanie z geometrii analitycznej (co prawda z gwiazdką, ale jednak) za łatwe na konkurs, i wykorzystuje informacje ze starszych klas

Adamm: wiem, bo pamiętam jak rozwiązywałem je w zbiorze zadań

Pełcio: no właśnie o to chodzi, ono jest łatwe dla kogoś kto już przeszedł tą geometrię analityczną, ale dla kogoś kto jej nigdy nie widział niekoniecznie, to zadanie właśnie pojawiło się na konkursie, ale na szczęście tylko raz

Pełcio: Saizou dochodzę do takiego czegoś:

a+b		2P
	<
2P		a+b+c

Saizou : Popraw się, dochodzisz do czegoś takiego

a+b+c		a+b		a+b+c
	≤		<
4P		2P		2P

Pełcio: A, ok, raz nie odwróciłem no to między II a III to widać, a między I a II? albo źle liczę bo już jestem zmęczony, albo coś takiego zostaje a+b>c czyli nierówność trójkąta, czyli prawda?

Saizou :

Pełcio: A to pierwsze zadanie to ma ktoś pomysł? bo nie za bardzo wiem jak to ruszyć

jc: lewa strona = p + q √2 = 4 + √5, p, q − liczby wymierne. p − 4 = √5 − q √2, q≠0, bo √5 jest liczbą niewymierną (5 + 2 q² − (p−4)²)/(2q) = √10, sprzeczność bo √10 jest liczbą niewymierną

Pełcio: 2 pytania mam 1. dlaczego lewą stronę zapisałeś w takiej postaci? 2. co się stało między drugą a trzecią linijką?

Adamm: przepraszam, ale się wtrącę 1. dla uproszczenia, rozwiń potęgi, wyjdzie to samo 2. operacja podnoszenia do kwadratu

Adamm: sam bym o tym nie pomyślał, ale rozumieć a wymyślić to co innego

Pełcio: no, ciekawy pomysł, dziękować

Pełcio: Jeszcze spytam o to... Wiem, że można to zrobić tą pochodną, ale nie wiem czy ją umiem tworzyć, dlatego da się skończyć to rozumowanie? x4+2ax+b=0 <−−−− udowodnij, że jeśli ma pierwiastek dwukrotny, to 27a4−16b3=0 Zapisuję w postaci: (x−c)²(x−y)(x−z)=0 po wymnożeniu mam: x4−(z+y+2c)x3+(yz+2zc+2yc+c²)x2−(2cyz+zc²+yc²)x+c²yz=0 z+y+2c=0 ⋀ yz+2zc+2yc+c²=0 ⋀ −2a= 2cyz+zc²+yc² ∧ c²yz=b i teraz jak wyznaczę 1 literkę z pierwszego i wstawię do 2 to wychodzą brzydkie rzeczy, da się to jakoś ładnie skończyć?

Adamm: nie bój się pochodnej napisałem, pochodna sumy to suma pochodnych, stałą możesz wynieść przez nawias, (xⁿ)'=nxⁿ⁻¹ (x⁴+2ax+b)'=(x⁴)'+(2ax¹)'+(bx⁰)'=4x³+2a*(x¹)'+b*(x⁰)'=4x³+2a nie musisz pisać tych potęg, pomyślałem że może być ci łatwiej

Pełcio: właśnie dlaczego to b znika? skoro przy nim jest x⁰ (=1) ?

Adamm: pochodna to to jak szybko zmienia się funkcja dlatego używa się jej do wyznaczania monotoniczności funkcja stała się nie zmienia, pochodna wynosi 0

Adamm: co jest zgodne ze wzorem który ci podałem, poza punktem x=0 (x⁰)'=(0*x⁻¹)'=0 tyle że dla x=0 również pochodna wynosi 0 (pochodną tak naprawdę liczymy w punktach, ale przedstawiamy ją jako funkcję)

Pełcio: no tak, ok będę tak robił w razie czego dobra, koniec już tego, dobranoc dzięki za pomoc ze wszystkimi tymi zadaniami

jc: x⁴+2ax+b=0 4x³ + 2a =0 x³ = −a/2 b = −(2a−a/2)x = −3ax/2 b³ = −27a³ x³/8 = −27 a³ (−a/2) /8 = 27a⁴/16 27 a⁴ = 16 b³