w ostroslupie prawidlowym czworokatnym michałek: W ostrosłupie prawidlowym czworokatnym wysokosc sciany bocznej ma dlugosc 3√5 i tworzy z wysokością ostrosłupa kąt α taki, że sin α= 2/√5. Oblicz pole powierzchni bocznej tego ostrosłupa Proszę o rozwiązanie tego zadania z obliczeniami zaznaczylem na rysunku kąt i tego sinusa, i do pitagorasa powinnem wpisac x²+2²=(√5)² ?

michałek: x wychodzi 1

Jerzy:

x
	= sinα ... i teraz policz x
3√5

michałek: no ale z pitgorasa wyszlo mi wczesniej ze x² = 1, to dobrze czy zle?

michałek: x=6?

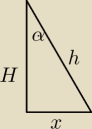
Jerzy: A do czego ci tu potrzebny Pitagoras ? H − wysokość bryły h − wysokość ściany bocznej x − połowa krawędzi podstawy

x
	= sinα
h

michałek: to ja juz nic nie rozumiem, czyli x*√5=2*3√5

Jerzy: Czyli: x = 6 Podstawa bryły ma krawędź: a = 2*x = 12

michałek: i teraz obliczyc pole powierzchni bocznej tylko tak?

michałek: Pb=4*pole trojkata

Jerzy: Tak.

stifler: to Pb wynosi 36?

Jerzy:

	1
Pb = 4*		*12*3√5 = ....
	2