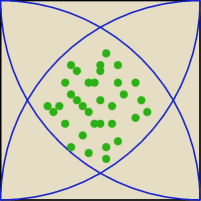
 Oblicz zamalowane pole w kwadracie o bokach=a
Starałem się wyjść z odejmowania pola wycinka kołowego od pola kwadratu, jednak brakuje mi tych
"listków" wychodzących od wierzchołków kwadratu.
Myślę, że rownanie powinno wyglądać tak: Pzaznaczone = Pkwadratu − 2PB −Px
gdzie PB = a2(1−1/4π)
a Px= nie mam pojęcia
Oblicz zamalowane pole w kwadracie o bokach=a
Starałem się wyjść z odejmowania pola wycinka kołowego od pola kwadratu, jednak brakuje mi tych
"listków" wychodzących od wierzchołków kwadratu.
Myślę, że rownanie powinno wyglądać tak: Pzaznaczone = Pkwadratu − 2PB −Px
gdzie PB = a2(1−1/4π)
a Px= nie mam pojęcia 
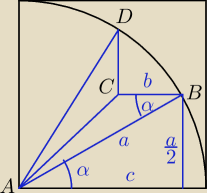 Poszukiwane pole = 4*(pole wycinka koła o promieniu a i kącie α=30o − 2*pole ΔABC)
Poszukiwane pole = 4*(pole wycinka koła o promieniu a i kącie α=30o − 2*pole ΔABC)
| a2*α | ||
pole wycinka koła = | ||
| 2 |
| a*b*sinα | a√3 | a | ||||
pole trójkąta ABC = | b = | − | ||||
| 2 | 2 | 2 |
| π | ||
pole = a2(1 + | − √3) | |
| 3 |