trygonometria asurbanipal: Funkcja f określona jest wzorem f(x) = sin x, dla x∊<0;2π>. Rozwiąż nierówność f(2x)≥2(f(x))². Podstawiam: sin 2x ≥ 2 sin² x i przekształcam: 2 sin x cos x ≥ 2 sin² x 2 sin x cos x − 2 sin² x ≥ 0 2 sin x (cosx−sinx) ≥ 0 ⇔ sin x (cosx−sinx) ≥ 0 ⇒

⎧	sin x ≥ 0
⎩	cos x − sin x ≥ 0	lub

⎧	sin x ≤ 0
⎩	cos x − sin x ≤ 0

i tutaj pojawia się problem z drugim równaniem (niezależnie czy większe czy mniejsze). Jak policzyć równanie sin x = cos x ?

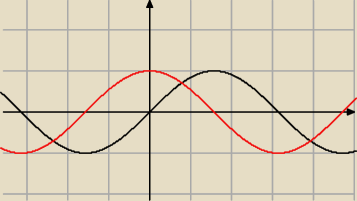piotr: Patrz na wykres.

piotr:

karty do gry : sin2x ≥ 2sin²x

	1 − cos2x
sin2x ≥ 2 *
	2

sin2x + cos2x ≥ 1

	π		√2
sin(2x +		) ≥
	4		2