,.,., Pełcio: Nowy temat, bo daleko w dół trzeba jechać. Mam jeszcze takie zadania, które nie za bardzo wiem jak ruszyć. 1. Udowodnij, że jeżeli a,b,c,d są całkowite i ciąg (a,b,c,d) jest ciągiem arytmetycznym, to liczba abcd+(a−b)⁴ jest kwadratem liczby całkowitej. 2. Dowieść, że jeżeli liczby a,b,c z których żadna nie jest zerem, spełniają równanie a³b³+b³c³+c³a³= abc(a³+b³+c³), to można je tak uszeregować, że utworzą ciąg arytmetyczny. 3. Dwa okręgi o promieniach r i R są stycznie zewnętrznie. Poprowadzono zewnętrzną styczną do obu okręgów. Oblicz promień okręgu wpisanego w powstały trójkąt krzywoliniowy. Oprócz tego, bardzo mnie ciekawi jakiś punkt zaczepienia chociaż do tego zadania: 4. Wykaż, że jeżeli boki i promień okręgu wpisanego w trójkąt mają całkowite długości, to obwód trójkąta jest liczbą parzystą. Jakby ktoś miał chwilkę czasu i chęci do pomocy..

Tadeusz: 4) Zrób rysunek a zobaczysz:

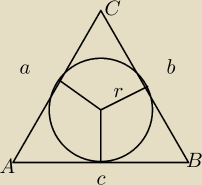
Pełcio: a,b,c∊ ℤ r∊ℤ

	a+b+c
P=		*r
	2

ale jak uzasadnić że to będzie parzyste?

g:

	a+b+c
4)		*r = √p(p−a)(p−b)(p−c) p = (a+b+c)/b
	2

z tego można wyznaczyć r w funkcji a,b,c

	abc
r2 = (ab+bc+ca) −		− p2
	p

jeśli a+b+c jest parzyste, to p jest całkowite i r² ma szansę (nie musi) być całkowite.

	abc
jeśli a+b+c jest nieparzyste, to p = n+1/2 i wtedy liczba		+ (n2+n+1/4)
	n+1/2

nie ma szans na bycie całkowitą.

Pełcio: ale np. a+b+c= 14, r=2 i działa

g: ale dlaczego "ale"? przecież 14 to liczba parzysta.

g: 1. a(a+r)(a+2r)(a+3r)+r⁴ = a⁴+6a³r+11a²r²+6ar³+r⁴ = (a²+3ar+r²)²

Pełcio: Może ktoś to sprawdzić? Mianownik pewnego nieskracalnego ułamka, będącego ilorazem dwóch liczb naturalnych, jest większy o 8 od kwadratu licznika tego ułamka. Jeżeli mianownik tego ułamka zmniejszymy o 4, to

	1
otrzymamy liczbę wiekszą od		, a jeśli licznik tego ułamka zwiększymy o 1 i mianownik
	5

	1
zmniejszymy o 6, to otrzymamy liczbę mniejszą od		. Co to za ułamek?
	2

	x
no to mamy ułamek		, x∊ℕ, y∊ℕ
	y

y=x²+8

x		1
	>
y−4		5

	x		1
1.		>
	x2+4		5

	x+1		1
2.		<
	x2+2		2

po przekształceniach, z pierwszej nierówności mam x∊(1,4), a z drugiej x∊(0,2), część wspólna to x∊(1,2)− tylko problem taki że nie ma tu żadnej liczby naturalnej... co robię źle?

Adamm: po primo czemu y=x²+8

	x
powinno być		=x2+8
	y

Adamm: nie, dobrze źle zobaczyłem

Pełcio: Ok, już widzę błąd. Dziękuję g za 1 zadanie, w 4 pomyliłem się, aczkolwiek myślę, że musi istnieć takie pewne rozwiązanie tego zadania, bez rozważania przypadków, że jeśli a+b+c jest parzyste to coś tam... Ale nie mówię, że nie masz racji, bo tego nie wiem W każdym razie, dzięki.

Adamm: źle policzona druga nierówność

Pełcio:

	3
Tak, tak, już poprawiłem i wyszedł ułamek		.
	17

Rafal: Szkic (3) Szukasz długości promienia okręgu stycznego do danych okręgów i do danej prostej. Po poprowadzeniu wszystkich możliwych promieni do wszystkich możliwych punktów styczności powinieneś zobaczyć trzy trapezy prostokątne: dwa małe i jeden duży. W każdym z nich poprowadź wysokości, które podzielą je na prostokąty i trójkąty prostokątne. W każdym z tych trójkątów zastosuj twierdzenie Pitagorasa − będziesz musiał wprowadzić trochę dodatkowych oznaczeń, ale nimi się nie przejmuj. Powinieneś dostać trzy równości, z których dasz radę wybrnąć.

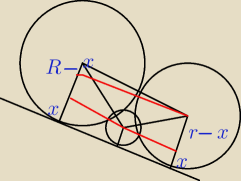
Pełcio: coś takiego?

Pełcio: o chyba działa dzięki

Adamm: a³b³+b³c³+c³a³= abc(a³+b³+c³) a³b³+a³c³+a⁶+b³c³−a⁶=abc(a³+b³+c³) a³(a³+b³+c³)−abc(a³+b³+c³)−a⁶+b³c³=0 a(a²−bc)(a³+b³+c³)+b³c³−a⁶=0 a(a²−bc)(a³+b³+c³)+(bc−a²)(b²c²+bca²+a⁴)=0 a²=bc lub a*(a³+b³+c³)−b²c²−bca²−a⁴=0 a²=bc lub ab³+ac³−b²c²−bca²=0 Δ=(b³+c³)²−4b³c³=(b³−c³)²

	b3+c3±(b3−c3)
a=
	2bc

a²=bc lub b²=ac lub c²=ab zapewne tam miało być "ciąg geometryczny"

Pełcio: tak, tak, geometryczny, zgubiłem się w 3 linijce od dołu, co to za delta?

Rafal: Pełcio, masz może zadania z tegorocznej edycji tego konkursu?

Adamm: potraktowałem to jak równianie kwadratowe względem a powinienem był napisać indeks dolny

Pełcio: aa, ok Adamm, fajne, ale już dosyć ciężki pomysł żeby dopisać to a⁶ Rafal, finał (4 etap) konkursu jest za 2 dni. Ostatnio zrobiłem porządek w makulaturze i powywalałem niestety te papierki... Znalazłem tylko zadania z etapu szkolnego

Rafal: OK, po prostu byłem ciekaw. Sam kiedyś robiłem z niego sporo zadań i bardzo mi pomogły

Rafal: Oczywiście nie w konkursie, tylko ogólnie.

Pełcio: Podam Ci ze szkolnego. 1. Wiadomo że xyz=1.

	1		1		1
Oblicz:		+		+
	1+x+xy		1+y+yz		1+z+zx

2. Rozwiązaniami równania o współczynnikach całkowitych x²+ax+1−b=0 są liczby naturalne. Udowodnij, że liczba a²+b² jest złożona. 3. W kwadrat ABCD o boku długości 2a wpisano okrąg. Oblicz długość cięciwy wyciętej przez ten okrąg z odcinka łączącego wierzchołek A ze środkiem boku CD.

Pełcio: Jak znajdę powiatowy i rejonowy to wpiszę. Ale ogólnie nie były trudne, bo przeszedłem

Adamm: a jaki to jest konkurs?

Pełcio: PKM− Podkarpacki Konkurs Matematyczny

Adamm: cieszysz się że przeszedłeś?

Pełcio: całkiem fajny konkurs dla rozrywki, może do matury coś nauczy

Rafal: Dzięki No cóż, mi też by pewnie sporo zajęło, zanim bym znalazł ciąg równości Adamma (nie mam talentu Ale możesz też pomyśleć w ten sposób: mamy uzasadnić, że albo a²=bc, albo b²=ac, albo c²=ab, bo zmienne a,b,c są symetryczne. Co ciekawego powiesz o równości (a²−bc)(b²−ac)(c²−ab)=0?

Adamm: szczerze? wątpię

Pełcio: Nawet jak nie, to sobie porobiłem zadania Znaczy nie chodzi mi o typ zadań, bo są całkiem inne niż maturalne , ale ogólnie o pomysły i jakieś myślenie

Pełcio: Rafal co o niej wiemy? ja wiem tylko tyle: a²=bc lub b²=ac lub c²=ab

Adamm: chodzi o to że nierówność napisana przez Rafala jest taka sama jak nierówność z której wychodziliśmy w zadaniu 2

Adamm: można pomyśleć że musi być a²=bc lub b²=ac lub c²=ab i stąd wywnioskować że nasze równanie (miałem na myśli równanie w tamtym poście tak btw.) przedstawia dokładnie to

Pełcio: Rzeczywiście, nawet już sobie to kiedyś napisałem, ale tak niepodobne mi się to wydawało, że nawet nie mnożyłem, a jednak o to chodzi Ale co wtedy w rozwiązaniu napisać? Może to być od razu pierwsza linijka rozwiązania i druga, że a²=bc lub b²=ac lub c²=ab i tyle?

Adamm: wystarczy napisać że (a²−bc)(b²−ac)(c²−ab)=0 ⇔ cokolwiek tam było

Pełcio: Albo w sumie lepiej byłoby od tyłu zrobić, z dopisywaniem, tak jak zrobiłeś.

Pełcio: Ja jeszcze nie miałem ciągów i myślałem, że coś z nich trzeba wiedzieć, ale w sumie do tych zadań nie

Pełcio: Mam jeszcze pytanie do tego zadania (już kiedyś je tu dawałem):

	a−b		b−c		c−a
Wykaż, że jeśli		+		+		=0 to co najmniej dwie spośród liczb
	1+ab		1+bc		1+ac

a,b,c są równe. po długim mnożeniu zostało mi tyle: a²(c−b)+b²(a−c)+c²(b−a)=0 czyli mamy a=0 ⋁ c=b itd. i to a tu wgl nie wpływa na zadanie tak?

Adamm: a=0 ⋁ c=b skąd tak wnioskujesz? nie pogrupuj to jeszcze

Adamm: albo, możesz wziąć przykład z wcześniejszego przykładu, i tak jak wskazał Rafal, wymnożyć odpowiednie wyrażenia

Pełcio: ok, po dodaniu i odjęciu abc doszedłem do (a−c)(b−a)(b−c)=0

Adamm:

Pełcio: A takie zadanie? Udowodnij, że jeżeli liczba całkowita podzielna przez 3 jest sumą pięciu kwadratów liczb całkowitych, to co najmniej dwa z tych kwadratów są podzielne przez 9. Ustaliłem tylko tyle, że kwadrat z liczby przy dzieleniu przez 3 daje resztę 0 lub 1, a nasza liczba (która jest sumą tych 5 liczb) przystaje do 0(mod 3). Czyli mamy dwa przypadki: 1. Dwie liczby które dzielą się przez 3 i trzy liczby które dają resztę 1. 2. Wszystkie liczby dzielą się przez 3. Ale jak udowodnić podzielność przez 9?

Adamm: jeśli kwadrat dzieli się przez 3 to również przez 9 to chyba oczywiste

Pełcio: aaaaaaaaa... i to jak bym dopisał to już skończone zadanie?

Adamm: oczywiście, liczby całkowitej myślę że tak, ale nie czytam w myślach tym co takie zadania sprawdzają

Pełcio: o, albo żeby było ładniej to można by się było bawić w zapisywanie tych liczb tak: a²+b²+c²+d²+e²=f w 1 przypadku a=3k b=3l c= 3m+1 d=3n+1 e= 3o+1 i popodnosić i wyciągnąć 3, to będzie przejrzyściej, tak mi się wydaje przynajmniej

Pełcio: jeszcze w tym zadaniu alfabetu by nie brakło

Adamm: no nie wiem, czy to aby na pewno byłoby bardziej przejrzyste? możliwe że dałoby odwrotny efekt

Pełcio: a może i tak, ale obydwa powinny chyba zostać uznane

Pełcio: Wyznacz wszystkie wartości wymierne parametru a , dla którego funkcja f(x)= ax²+(a+1)x+a−1 ma wszystkie miejsca zerowe całkowite. Masz jakiś pomysł Adamm?

Adamm: a=p/q gdzie p/q jest nieskracalny, q≠0 f(x)=px²/q+(p+q)x/q+(p−q)/q f(x)=0 px²/q+(p+q)x/q+(p−q)/q=0 dla p=0 mamy funkcje liniową oraz całkowite miejsce zerowe od teraz założymy ze p≠0 x²+(p+q)x/p+(p−q)/p=0 teraz widać że jeśli miejsca zerowe istnieją i są całkowite to (p−q)/p oraz (p+q)/p muszą być całkowite zatem q/p musi być całkowite skąd p=1 (założyliśmy że p/q jest nieskracalny) x²+qx−q=0 x₁+x₂=−q, x₁*x₂=−q x₁+x₂=x₁*x₂ x₁|x₂ oraz x₂|x₁ ⇒ x₁=±x₂ przy czym dla − mamy sprzeczność z założeniem x₁=−q/2 oraz x₁²=−q q=−4 jedyne rozwiązania to a=0 oraz a=−1/4

Pełcio: 7 linijka, dlaczego przed x² już nic nie ma?

Adamm: x²+qx−q=0 od tego momentu pomyłka x²+(1+q)x+(1−q)=0 x₁x₂=1−q, x₁+x₂=−1−q x₁x₂=x₁+x₂+2 x₁(x₂−1)=x₂+2

	x2+2		3
x1=		=1+
	x2−1		x2−1

x₂−1=±1, x₂−1=±3 x₁=0 lub x₂=2 lub x₂=−2 lub x₂=4 (0; −2), (2; 4) takie mamy możliwe miejsca zerowe q=1 lub q=−7 a=0 lub a=1 lub a=−1/7

Adamm: czemu miałoby być? chcemy się tego pozbyć

Adamm: rozpatrzyliśmy przypadek gdy p=0, możemy się tego pozbyć

Adamm: pomyłka jeszcze raz, tam przecież powinno być q x²+q(p+q)x/p+q(p−q)/p=0 znowu jak wcześniej q(p+q)/p oraz q(p−q)/p musi być całkowite, stąd q/p musi być całkowite ⇒ p=1 x²+(q+q²)x+q−q²=0 x₁+x₂=−q−q², x₁x₂=q−q² x₁+x₂=−q(1+q), x₁x₂=q(1−q) q|x₁+x₂, q|x₁x₂ q|x₁²+x₁x₂ q|x₁² q|x₁ podobnie q|x₂ q|1−q, q|1, q=±1 cóż, wyszło mi coś innego a=0, a=1 lub a=−1

Pełcio: ale to się wlicza do delty, to nie robi żadnej różnicy?

Adamm: mam nadzieję że nie zamieszałem aż tak bardzo, ale musisz zrozumieć że jest dosyć późno na takie rzeczy

Adamm: masz na myśli rozpatrywanie wzorów Viete'a bez pierwszego sprawdzenia czy pierwiastki istnieją? mamy skończoną ilość rozwiązań, zawsze możemy sprawdzić do równania

Adamm: sprawdź rachunki jeszcze raz, ja już będę powoli się kładł, dobranoc

Pełcio: mamy postać początkową ax²+(a+1)x+a−1

	p
za a podstawiamy
	q

więc dlaczego tamta postać to jest 1x²+ (...) faktycznie jest chyba za późno, już mi mózg nie pracuje

Pełcio: dobranoc i dziękuję

jc: a=0, x=1 a≠0 ax²+(a+1)x+a−1 = a(x−k)(x−m) = ax²−(k+m)ax + kma a+1= −(k+m)a a−1=kma 2=−k−m+km 3=(k−1)(m−1) k=4, m=2 lub k=0, m=−2 W pierwszym przypadku a=−1/7, w drugim a=1.

Adam: jednak w drugim było dobrze, pomyliłem się z tym q

Pełcio: a k=−2 i m=0 oraz k=2 i m=4, to pewnie się połączy z tamtymi i a wyjdzie takie samo tak? dziękuję jc

jc: Tak, jak piszesz. k i m występują symetrycznie.