planimetria xxx: Na bokach: AB, BC i AC trójkąta równobocznego ABC wybrano odpowiednio punkty K, L, i M w taki sposób, że ^|AK|_|KB|=^|BL|_|LC|=^|CM|_|MA|=¹₂. Punkty wspólne odcinków AL, BM i CK wyznaczają wierzchołki trójkąta PQR. Oblicz stosunek pola trójkąta PQR do pola trójkąta ABC.

xxx: Tylko co teraz?

xxx: Czy ktoś mógłby mnie chociaż naprowadzić na jakiś tor?

xxx: .

xxx: Odpowiedź to ¹₇

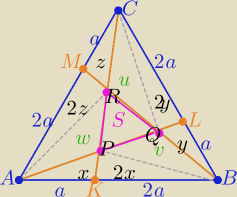Eta: Na rys. oznaczyłam pola odpowiednich trójkątów literkami : x, 2x, y,2y, z,2z,w,u,v i S 1/ w ΔACK i BCK ; 2(3z+x+w)=3y+2x+u+v+S ⇒ 6z+2w=3y+u+v+S w ΔBCM i BAM 2(3y+u+z)=3x+2z+w+v+S ⇒ 6y+2u=3x+w+v+S wΔABL i ACL 2(3x+y+v)=3z+2y+w+u+S ⇒ 6x+2v=3z+w+u+S dodając stronami : 3(x+y+z)= 3S ⇒ x+y+z=S podobnie w trójkątach ABR : 2(w+x)=2x+v+S ⇒ 2w=v+S CAQ : 2(z+u)=2z+w+S ⇒ 2u=w+S CPB : 2(v+y)=2y+u+S ⇒ 2v=u+S dodając stronami u+w+v=3S P(ABC)= 3x+3y+3z+u+w+v+S = 3S+3S+S

	1
P=7S ⇒S=		P
	7

Może Mila poda prostszy sposób ( z wykorzystaniem własności trójkąta równobocznego

Mila: Wczoraj miałam problem z rysunkiem, dzisiaj też coś mi nie wchodzi. Nie wydaje mi się, aby mój sposób był prostszy, ale napiszę. P_ΔABC=P 1) Rysunek I

	1		1
PΔABL=		P⇔3s+u=		P /*3
	3		3

	2		2
PΔKBC=		P⇔2s+3u=		P⇔
	3		3

9s+3u=P

	1
2s+3u=		P
	3

=========stąd

	1		1
s=		P⇔PΔAKP=		P
	21		21

======================= 2) rysunek II

	1
PAPRM=		P−2s=v
	3

	7		2		5
v=		P−		P=		P
	21		21		21

P=3s+3v+x

	3		15
P=		P+		P+x
	21		21

	3		1
x=		P ⇔x=		P
	21		7

x		1
	=
P		7

============

Eta: Witam Ładnie

Mila: Hej

xxx: Ślicznie dziękuję

Mila: