sąsiednie ściany boczne ostrosłupa prawidłowego sześciokątnego o krawędzi podsta 123: sąsiednie ściany boczne ostrosłupa prawidłowego sześciokątnego o krawędzi podstawy długości a i wysokości H tworzą kąt dwuścienny o mierze alfa. Wyznacz cos alfa

123: Ktoś pomoże?

123: f5

123: nikt ?

Eta:

	H2−3a2
cosα=
	H2+3a2

Czy taką masz odpowiedź?

Mila: Problem polega na wykonaniu dobrego rysunku. Może uda się.

123: Nie mam odpowiedzi A jak do tego doszlas?

Eta: Drugi raz liczyłam i mam inny wynik Poczekamy na Milę

Eta:

	2H2+a2
cosα=
	4H2+3a2

Ciekawe czy taki wynik otrzyma Mila

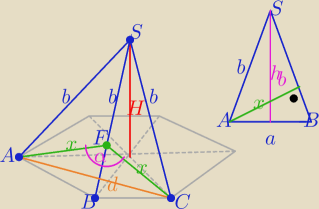
Eta: Z tw. kosinusów w ΔACF

	x2+x2−d2		d2
cosα=		= 1−
	2x2		2x2

d=(a√3)²=3a²

	a		a2
hb2=b2−(		)2 = b2−
	2		4

	4H2+4a2−a2		4H2+3a2
i b2=H2+a2 to h2=		=
	4		4

	x*b		a*h
Pole ściany : P=		i P=
	2		2

	a2*h2
zatem: x2*b2=a2*h2 ⇒ x2=
	b2

i dokończ.....................

	3a2
cosα= 1−		=....................
	2x2

Mila: Eto, mam rysunek i wynik, ale mam ujemny wynik i taki chyba powinien być. Liczę jeszcze raz.

Eta: No właśnie ... cosα −−− powinien być ujemny coś nie tak liczę? Pokaż swoje obliczenia

Mila:

	a√3
|BD|=2*		=a√3
	2

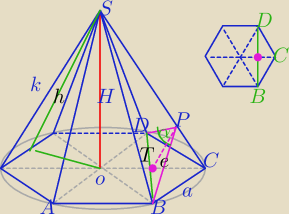
1) WΔBDP: |BD|²=e²+e²−2*e*e*cosα (a√3)²=2e²−2e²*cosα⇔ 3a²=2e²*(1−cosα)

	3a2
1−cosα=
	2e2

	3a2
1−		=cosα
	2e2

2) k²=H²+a²

	a√3		3
h2=(		)2+H2=		a2+H2
	2		4

3) Porównanie pola ΔBCS:

1		1
	*a*h=		*e*k
2		2

a*h=e*k /² a²*h²=e²*k²

	3   a2*(H2+ a2)   4
e2=
	H2+a2

4)

	H2+a2
cosα=1−3a2*
	3   2*a2*(H2+ a2)   4

	2H2+3a2
cosα=−
	4H2+3a2

Jednak może być pomyłka w ostatnich obliczeniach. Sprawdzaj maturzysto.

Eta: Sposób taki sam ....... gdzieś zgubiłam minusa

Mila: Liczyłam też inaczej, ale nic nie było prościej. Jutro przeliczę innym sposobem, może |TP| obliczę. Dobranoc

Eta: Dobranoc