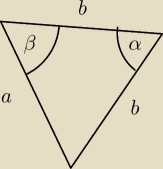
Dowód, planimetria, trójkąt bc = a^2 - b^2 to α = 2β SEKS INSTRUKTOR : W trójkącie oznaczone są boki : a, b, c. Kąt α leży naprzeciwko boku a, kąt β naprzeciwko boku b. Wykaż, że jeżeli bc = a² − b² to α = 2β Robiłem już mnóstwo razy, różnymi sposobami. Cały czas wychodzi mi tożsamość trygonometryczna. Prosze o pomoc.

Adamm: stosując tw. Sinusów dostajemy sinβ*sin(α+β)=sin²α−sin²β sinβ*sin(α+β)=(sinα+sinβ)(sinα−sinβ) sinβ*sin(α+β)=4sin([α+β]/2)cos([α+β]/2)sin([α−β]/2)cos([α−β]/2) sinβ*sin(α+β)=sin(α+β)*sin(α−β) sin(α+β)=0 lub sinβ=sin(α−β) α+β=πk lub 2β=α+2kπ lub α=π+2k

Mila: bc = a² − b² to α = 2β

a
	=2R ⇔a=2R*sinα
sinα

b=2R*sinβ c=2R*sin (180−(α+β))⇔c=2R*sin(α+β) (2Rsinα)²−(2Rsinβ)²=2R*sinβ*2R*sin(α+β)⇔ sin²α−sin²β=sinβ*sin(α+β) (sinα−sinβ)*(sinα+sinβ)=sinβ*sin(α+β)

	α+β		α−β		α+β		α−β
2cos		*sin		*2*sin		*cos		=sinβ*sin(α+β)
	2		2		2		2

sin(α+β)*sin(α−β)=sinβ*sin(α+β) /: sin(α+β) [ α+β≠0 w trójkącie] sin(α−β)=sinβ w Δ zachodzi równość: α−β=β⇔α=2β ===========

SEKS INSTRUKTOR : Dziękuję serdecznie

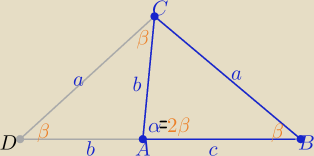
Eta: Można też tak: W odwrotną stronę Jeżeli α=2β to dorysowujemy trójkąt DAC równoramienny Trójkąty DBC i DAC są równoramienne i podobne z cechy (kkk)

	a		b
zatem		=		⇒ bc+b2=a2⇒ bc=a2−b2
	b+c		a