funkcja logarytmiczna, algebra liniowa Bartimaeus: Zaznacz w układzie współrzędnych zbiór wszystkich punktów, których współrzędne x,y spełniają nierówność log_1/2(|y|−1)>=x

Adamm: |y|−1>0 y∊(−∞;−1)∪(1;∞) log_1/2(|y|−1)≥x

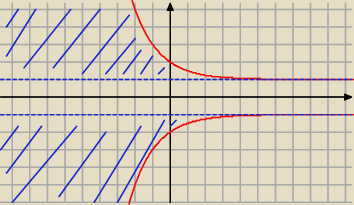
	1
|y|−1≤(		)x
	2

	1
|y|≤(		)x+1
	2

	1		1
−(		)x−1≤y≤(		)x+1
	2		2

Mila: log_(1/2)(|y|−1)≥x 1) |y|−1>0⇔|y|>1 y<−1 lub y>1 2)

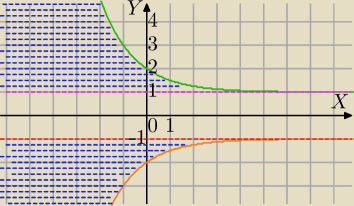
	1
log(1/2)(|y|−1)≥log(1/2)(		)x⇔
	2

	1
|y|−1≤(		)x⇔
	2

	1
|y|≤(		)x+1
	2

a)

	1
|y|=y dla y≥0 i y>1⇔obszar nad prostą y=1 i poniżej wykresu funkcji y=(		)x+1
	2

b) |y|=−y dla y<0 i y<−1

	1
−y≤(		)x+1⇔
	2

	1		1
y≥−(		)x−1 obszar nad wykresem funkcji y=−[(		)x+1] i poniżej prostej y=−1
	2		2

Bartimaeus: Dzięki, nie pomyślałem o tym przekształceniu do (1/2)^x