planimetria
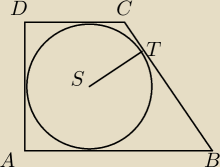
Krakus: W trapez prostokątny ABCD wpisano okrąg, przy czym punkt S jest środkiem tego okręgu, a punkt
T jest punktem styczności okręgu wpisanego z dłuższym ramieniem BC . Oblicz pole tego
trapezu, jeśli |SC | = 10 i |BT | = 8√ 5 .
16 kwi 14:57
Adamm: z podobieństwa
r
4=320*(100−r
2)
r
4+320r
2−32000=0
r=4
√5
dalej już prosto
16 kwi 15:26
tyokke:
ale r powinno wyjść chyba 8
√5 skoro punkt T jest punktem styczności?
16 kwi 15:41
Adamm: tyokke, to do mnie nie przemawia
16 kwi 15:43
tyokke:
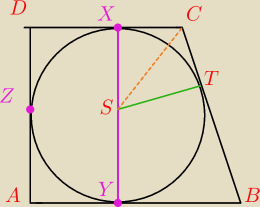
jak dla mnie to powinno być tak |ST| = r |XY| = 2r |ST|=|DX|=|DZ|=|ZA|=|AY| i teraz
kombinować wyliczanie |BT| |BY|
16 kwi 15:49
tyokke: ale niech ktoś mądry się wypowie
16 kwi 15:50
Adamm: ale nie podałeś żadnych konkretów
nie masz żadnych argumentów
16 kwi 15:51
Adamm: jeśli mówisz że r=8√5 to musisz to czymś najpierw podeprzeć
jak dla mnie rzucasz słowa na wiatr
16 kwi 15:52
tyokke: Boże, źle przeczytałem i zrozumiałem że w zadaniu jest napisane że odległość |ST| jest równa
8√5, przepraszam i zwracam honor
16 kwi 15:54
Adamm: zresztą, r nie może być równe 8√5, bo wtedy XSC nie może być trójkątem
16 kwi 15:55
tyokke: Mówię że źle przeczytałem, dlatego całe zadanie zacząłem rozwiązywać kompletnie inaczej
16 kwi 15:56
Adamm: napisałem post przed tym jak widziałem twój
rozumiem
16 kwi 15:56
Mila:
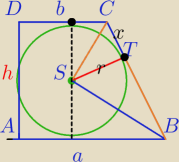
ΔBSC− Δprostokątny
|SC|=10
|BT|=8
√5
1)
r
2=x*8
√5
x
2+r
2=10
2⇔
x
2+8
√5x−100=0, x>0
Δ=720=36*20=36*4*5
√Δ=12
√5
| | −8√5−12√5 | |
x= |
| <0 lub x=2√5 |
| | 2 | |
2)
r
2=2
√5*8
√5=16*5⇔ r=4
√5
3)
h=8
√5
4)|BC|=2
√5+8
√5=10
√5
5)
a+b=c+d⇔a+b=10
√5+8
√5=18
√5
6)
P=320[j
2]
16 kwi 20:47
Mila:
PABCD=360[j2]
16 kwi 20:49
 ale r powinno wyjść chyba 8√5 skoro punkt T jest punktem styczności?
ale r powinno wyjść chyba 8√5 skoro punkt T jest punktem styczności?
 jak dla mnie to powinno być tak |ST| = r |XY| = 2r |ST|=|DX|=|DZ|=|ZA|=|AY| i teraz
kombinować wyliczanie |BT| |BY|
jak dla mnie to powinno być tak |ST| = r |XY| = 2r |ST|=|DX|=|DZ|=|ZA|=|AY| i teraz
kombinować wyliczanie |BT| |BY|
 ΔBSC− Δprostokątny
|SC|=10
|BT|=8√5
1)
r2=x*8√5
x2+r2=102⇔
x2+8√5x−100=0, x>0
Δ=720=36*20=36*4*5
√Δ=12√5
ΔBSC− Δprostokątny
|SC|=10
|BT|=8√5
1)
r2=x*8√5
x2+r2=102⇔
x2+8√5x−100=0, x>0
Δ=720=36*20=36*4*5
√Δ=12√5