trapez 1.167: Punkt S jest środkiem okręgu wpisanego w trapez ABCD (AB ∥ CD ). Wykaż, że trójkąt SBC jest prostokątny. Zadanie jest proste natomiast moje pytanie jest takie iz dlaczego sc i sb to dwusieczne bo w tresci zadania nie ma o tym kompletnie mowy dziekuje

Adamm: trójkąty ASC oraz BSC są przystające na zasadzie bbb ponieważ |AS|=|BS| oraz |CS|=|CS| oraz |BC|=|AC| (tw. Pitagorasa) z tego że są przystające, kąty SCA oraz SCB są równe, zatem CS jest dwusieczną tego kąta

g: To są dwusieczne z powodu podobieństwa odpowiednich trójkątów.

1.167: czyli to ze sa podobne to znaczy ze sa to dwusieczne

Adamm: ułóż poprawne logicznie zdanie, to ci odpowiem

Adamm: "czyli to ze sa podobne to znaczy ze sa to dwusieczne" to że są podobne trójkąty są podobne, tak znaczy że są to dwusieczne ... napisz porządnie, logicznego myślenia cię nie nauczę

1.676: Jasne moge sformułować inaczej zdanie. To ze cos jest logiczne dla Pana nie musi byc dla mnie i odwrotnie. Hmm nie moge dalej pojac tego dlaczego wykorzystujemy w tym zadaniu dwusieczne i skad wiemy ze one aie przetna w pkt s.

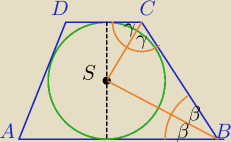
Mila: 1) Środek okręgu wpisanego w trapez leży w punkcie przecięcia dwusiecznych kątów wewnętrznych trapezu. 2) 2β+2γ=180 własność kątów przy ramieniu trapezu β+γ=90⇔ΔBSC− Δprostokątny.

1.676: Aha czyli poprotu jest taka wlasnosc ze srodek okregu wpisanego w trapez jest miejacem gdzie przecinaja sie dwusieczne ?

Adamm: "Środek okręgu wpisanego w trapez leży w punkcie przecięcia dwusiecznych kątów wewnętrznych trapezu." zgadzam się z tym całkowicie ale żeby nie było pytań na przyszłość, pozwolę sobie zastąpić słowo trapez na czworokąt

Adamm: dlaczego tak jest? z postu 14:20 powinieneś wiedzieć że mając 2 proste styczne do okręgu, odcinek między punktem przecięcia tych prostych, a środkiem okręgu pokrywa się z prostą będącą dwusieczną kąta powstałego przez te proste zatem dwusieczne dowolnego czworokąta do którego można wpisać okrąg muszą przecinać się w punkcie będącym środkiem okręgu wpisanego w ten czworokąt

Adamm: a jeśli już przy tym jesteśmy, podobna logika zadziała dla dowolnego wielokąta w który można wpisać okrąg