maturka Kacper: Zadanko świąteczne dla maturzystów Na kuli o promieniu R opisano prawidłowy ostrosłup sześciokątny, którego ściana boczna tworzy z płaszczyzną podstawy kąt a. Oblicz pole powierzchni bocznej i objętość tego ostrosłupa.

5-latek: A dla przedszkolakow masz tez ? Zdrowych i Wesolych Świat zycze .

Adamm:

	2R3(1+cosa)3
V=
	3sin2acosa

Kacper: Wynik z mojej książki, zakładając że jest ok, jest inny.

Mariusz: No i dla lepszej zabawy przydałaby się opcja ukryj dostępna na forach z texem

Adamm: Kacper, a jaki jest wynik?

Adamm: Mariusz, opcja ukryj byłaby przydatna, z tym się zgadzam

Kacper:

	4√3		4−sin2α
Odpowiedź wg podręcznika to:		*		*R3
	3		sin2

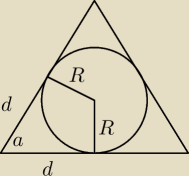
Adamm: tutaj d=x√3/2 gdzie x to bok podstawy

	x√3		x√3		x√3
z tw. Cosinusów mamy (		)2+(		)2−2*(		)2*cosa=
	2		2		2

	R2+R2cosa
=R2+R2+2R2*cosa ⇒ x2=		=
	3   3   − cosa 4   4

	4R2(1+cosa)2
=
	3sin2a

	2R(1+cosa)
x=
	√3sina

	x2√3		2√3R2(1+cosa)2
Pp=6*		=
	4		sin2a

h		R(1+cosa)
	=tga ⇒ h=
x√3   2		cosa

	1		2√3R2(1+cosa)2		R(1+cosa)
V=		*		*		=
	3		sin2a		cosa

	2√3R2(1+cosa)3
=
	3sin2acosa

pomyliłem się lekko przy liczeniu x, zapomniałem spierwiastkować 3, ale rozwiązanie nadal jest złe (?) mógłby ktoś wskazać błąd?

Adamm: ostatecznie tam miało być oczywiście R³ zamiast R²

Adamm: poprosiłem kogoś trzeciego żeby to rozwiązał, wynik miał taki sam

Adamm: Kacper, możesz napisać dokładnie odpowiedź? nie napisałeś jaki kąt przyjmuje sinus w mianowniku

Zdzisław: Czy wysokość ściany bocznej (w tym przypadku trójkąta równoramiennego) ostrosłupa jest prostopadła do promienia wpisanej kuli?

Adamm: powinna być

Kacper: Zjadło mi kąt, tam ma być alfa. Jutro sam policze i powiem co i jak. Zawsze może być błąd w książce

Kacper: Oblicz pole powierzchni bocznej i też porównamy wynik.

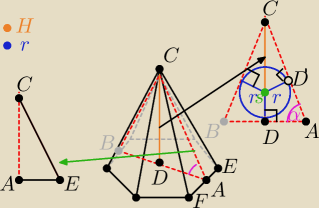
Zdzisław: Żeby obliczyć pole boczne potrzebuję wyznaczyć wysokość ΔFCE czyli odcinek |AC|

	|DA|		|FE|√3   2		|FE|√3
cosα =		=		⇒ |AC|=
	|AC|		|AC|		2cosα

	1		1		|FE|√3		|FE|2√3
PΔFCE=		*|FE|*|AC|=		*|FE|*		=
	2		2		2cosα		4cosα

Wiem wiem, że trzeba przez R wyrazić, ale może dzięki temu (o ile jest dobrze) ktoś na coś wpadnie

Adamm:

hboczna
	=sina
h

	R(1+cosa)sina
hboczna=
	cosa

	1		2√3R2(1+cosa)2
Pb=6*		*x*hboczna=
	2		cosa

Adamm: pomyliło mi się

h
	=sina
hboczna

R(1+cosa)
	=hboczna
cosa*sina

	1		2√3R2(1+cosa)2
Pb=6*		*x*hboczna=
	2		sin2acosa

Kacper:

	8√3
Pb=		*R2
	sin2α

Muszę pomyśleć czy to to samo, ale wątpię