Zadania optymalizacyjne majsa: Rozważmy te ostrosłupy prawidłowe czworokątne ,w których suma długości wysokości i krawędzi podstawy jest równa 8 cm. Spośród tych ostrosłupów wybrano taki że pole trójkąta , którego bokami są dwie krawędzie boczne i przekątna podstawy ostrosłupa , jest największe. A) Znajdź długość krawędzi podstawy i wysokość tego ostrosłupa B) oblicz objętość ostrosłupa

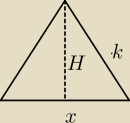
Jerzy: Podstawą jest przekatna kwadratu o boku a. Masz związek: a + H = 8 Wyraź pole trójkąta jako funkcję x i policz jej maksimum.