Geometria Analityczna Nieogarnięty: Wyznacz współrzędne punktów A,B przecięcia prostej o równaniu y=³₂x−9 z osiami układu współrzędnych.Wyznacz obwód trójkąta ABO , gdzie O jest początkiem układu współrzędnych oraz długość wysokości OC.

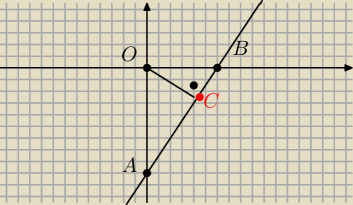
5-latek: Punkt przeciecia prostej y=1,5x−9 z osia oY ma wspolrzdne A=(0,−9) Punkt przeciecia prostej z osia OX ma wspolrzedne 1,5x−9=0 1,5x=9 ⇒x=6 czyli B=(6,0) Do obliczenia obwodu wzor na odleglosc dwoch punktow od siebie DO wyznaczenia wysokosci wzor na odleglosc punktu od prostej

Tadeusz: Możesz też przekształcić równanie proste do postaci odcinkowej

	x		y
3x−2y=18 ⇒		−		=1
	6		9

	1
Masz odcinki odłożone na osiach ... masz pole trójkąta S=		*6*9=27
	2

Znasz długość |AB|=√117=3√13 |OC| policz jako wysokość trójkąta (znasz pole i podstawę)

Nieogarnięty: Czyli mamy |AB|=3√13 |OB|=6 |AO|=9 O=|AB|+|OB|+|AO|=3√13+6+9=3√13+15

	3√13*√3		3√39
|OC|=h=		=
	2		2

dobrze