Znaleźć wartości najmniejszą i największą funkcji Beorn: Znaleźć wartości najmniejszą i największą funkcji f(x, y) = x² −y² w trójkącie o wierzchołkach (1, 1), (3, 1),(1, 3). Policzylem pochodne po x i y z funkcji i ulozylem uklad rownan z ktorego wyszlo mi ze x i y=0 Czy zadanie jest skonczone czy musze liczyc po granichach trojkata jeszcze?

Adamm: musisz liczyć po granicach trójkąta

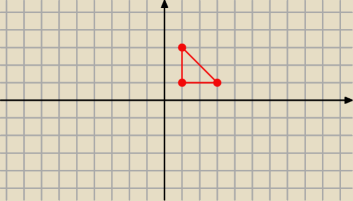
Adamm: x=1, y∊<1;3> y=1, x∊<1;3> y=−x+4, x∊<1;3>

Beorn: przy 1 wyszlo mi y=0 2. y=0 3. 8=0 sprzecznosc odpowiedz funkcja nie przyjmuje zadnych wartosci w trojkacie i na jego krawedziach?

Adamm: 1. x=1, y∊<1;3> f(1; y)=1−y² tutaj funkcja przyjmuje maksimum oraz minimum na krańcach f(1; 1)=0, f(1; 3)=−8 2. y=1, x∊<1;3> podobnie f(x; 1)=x²−1 f(1; 1)=0, f(3; 1)=8 3. y=−x+4, x∊<1;3> f(x; −x+4)=8x−16 nadal na krańcach (te same punkty co wcześniej) punkt (0; 0) jest poza dziedziną, nas nie obchodzi mamy minimum f(1; 3)=−8 oraz maksimum f(3; 1)=8

Beorn: Ja to robilem tak ze podstawialem np w 1.x=1 pod f(x,y) a pozniej liczylem z tego pochodna z ktorej liczylem niewiadoma f(1,y)= 1−y² (1−y²)'=−2y −2y=0 y=0 nie nalezy czy ta metoda jest zla? sam jej nie wymyslilem tylko tak gosciu tlumaczy w poradniku

Adamm: nie jest zła ale to że ekstremum z pochodnej nie należy do naszego przedziału, nie znaczy że funkcja nie przyjmuje wartości największej/najmniejszej

Adamm: i tak poza tym, to jest funkcja kwadratowa, można się obejść bez pochodnej

Beorn: to po co sie pochdna liczy zamiast od razu 1−y²=0 napisać?

Adamm: napisałeś głupotę, nie wiem co na to odpowiedzieć

Beorn: napisales ze moja metoda jest dobra ale podales mi inne rozwiazanie nie liczac pochodnej.Skad mam wiedziec kiedy ja liczyc a kiedy nie

Adamm: nie liczyłem pochodnej ponieważ to funkcja kwadratowa wiadomo kiedy funkcja kwadratowa przyjmuje minimum/maksimum jeśli przed sobą miałbym np. wielomian stopnia 3, sprawa miałaby się inaczej, i policzyłbym pochodną

Adamm: to że liczyłem inaczej, nie znaczy że twój sposób jest zły tutaj również możesz policzyć pochodną ale pochodna jest równa 0 gdy y jest poza przedziałem, więc funkcja przyjmuje największą/najmniejszą wartość dla krańców tego przedziału, w tym przypadku dla x=1 oraz x=3

Beorn: czyli pochdne liczyc tylko dla wielomianow powyzej 2 stopnia? majac np x⁶ to gdy policzyl bym pochodna z tego moglbym od razu podstawiac do rownania 6x⁵=0? czy może muszę schodzić pochodnymi aż do 2 stopnia

Adamm: jeśli masz ograniczenie, tak jak w tym przypadku, to nie interesuje cię czy jest to maksimum, minimum, czy coś innego możesz od razu podstawić wartość