W przedziale ruzamka: Rozwiąż równanie w przedziale <−π,2π> sinx=sin7π/6 Mi wychodzi {−5π/6, 7π/6} A w książce to nie są jedyne poprawne odpowiedzi Wyjaśni ktos?

Alky: No chyba nie ma specjanie co wyjaśniać.

	1
sinx=−
	2

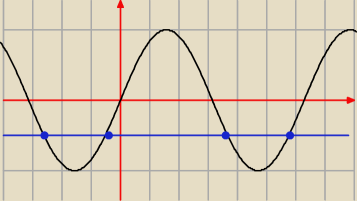
To równanie ma 3 rozwiązanie na przedziale <−π,2π> spójrz na wykres sinx (jeśli korzystasz z kart wzorów to tam jest, jeśli nie to znajdź na internecie )

	5
3 rozw:		π
	6

g:

ruzamka: Alky, odpowiedź to oprócz tego co napisałam, −π/6 i 11π/6 Więc chyba jednak potrzebne wyjasnienie

Mila: x∊<−π,2π>

	7π
sinx=sin		⇔
	6

	7π		7π		π
x=		+2kπ lub x=π−		+2kπ=−		+2kπ
	6		6		6

k=0

	7π		π
x=		∊D lub x=−		∊D
	6		6

k=1

	7π		π		11π
x=		+2π∉D lub x=−		+2π=		∊D
	6		6		6

k=−1

	7π		5π		π
x=		−2π=		∊<−π,2π> lub x=−		−2π∉D
	6		6		6

	5π		π		7π		11π
x∊{−		,−		,		,		}
	6		6		6		6

albo

	1
sinx=−		i x∊<−π,2π>
	2

Alky:

	1
Sorki, zagapiłem się. Myślałem o cosx=−		który miałby 3 rozw.
	2