pole obszaru
Remi: Oblicz pole obszaru ograniczonego punktami A=(2,4) B=(−1,5) C=(−3,1)
Może mi ktoś wytłumaczyć o co chodzi?
14 kwi 14:57
Jerzy:
To pole trójkąta o podanych wierzchołakach: A,B,C
14 kwi 14:58
Remi: W układzie współrzędnych?
14 kwi 14:59
Jerzy:
Na płaszczyżnie, obojetnie gdzie.
14 kwi 15:00
Remi: Czyli jak oznaczyć te punkty?
14 kwi 16:53
g:
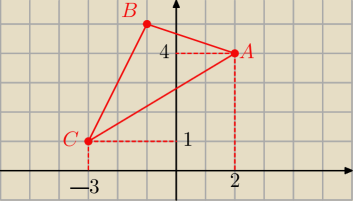
14 kwi 17:34
Adamm: najlepiej wyliczyć to ze wzoru (pomimo że to lekka głupota), bo w takich zadaniach liczy
się podejście geometrii analitycznej
14 kwi 17:35
Remi: Czy poprawne jest takie rozwiązanie
|AB|=
√(−1−2)2+(5−4)2
|AB|=
√10
Prosta AB ma równanie:
(y−4)(−1−2)−(5−4)(x−2)=0
−3y+12−x+2=0
Rysuje prostą k prostopadłą do AB i przechodzącą przez punkt C, więc ma ona równanie y=x+b
Punkt C należy do prostej k => 1=−3+b => b=4
Prosta k => y=x+4
Współrzędne punktu P:
y=x+4
y=7 => x=3
P=(3,7)
|PC|=
√(−3−3)2+(−1−7)2
|PC|=10
14 kwi 18:37
Adamm: "Rysuje prostą k prostopadłą do AB i przechodzącą przez punkt C, więc ma ona równanie y=x+b"
tutaj jest błąd, złe równanie prostej
14 kwi 18:41
14 kwi 18:43
Adamm: | | 1 | |
P= |
| |2*5+(−1)*1+(−3)*4−(−3)*5−2*1−(−1)*4|= |
| | 2 | |
=7
14 kwi 18:45
Adamm: prosta ta miałaby równanie y=ax+b, z warunku prostopadłości dostajemu
a*(−1/3)=−1 ⇒ a=3
taka prosta byłaby postaci y=3x+b
14 kwi 18:50
Remi: | | 1 | |
P= |
| |a1b2+b1c2+c1a2−c1b2−a1c2−b1a2| |
| | 2 | |
P=10
W ten sposób?
14 kwi 18:57
Adamm: źle podstawiłeś
14 kwi 18:58
Remi: Ale pod ten wzór należy podstawiać?
14 kwi 18:59
Adamm: tak
tutaj A=(2; 4), B=(−1; 5), C=(−3; 1)
można przyjąć
a1=2, a2=4, b1=−1, b2=5, c1=−3, c2=1
litery z indeksem dolnym 1 odpowiadają pierwszej współrzędnej, a z indeksem dolnym 2, drugiej
14 kwi 19:03
Remi: Już rozumiem. Dzięki za cierpliwość!

14 kwi 19:04
Mariusz:
Dane są trzy punkty więc najwygodniejszy będzie wzór wyznacznikowy
14 kwi 21:09

