pochodna kierunkowa dolan:

	√x
Wyznaczyć wszystkie punkty, w których pochodna kierunkowa funkcji f(x)=		w kierunku
	y

wersora (√2/2 ,√2/2) przyjmuje wartość 0.

Jerzy: I z czym masz problem ?

dolan: nie bardzo wiem o co chodzi w tym zapisie "w kierunku wersora" wersor ma dlugosc (1,1) tak? wiec czym jest kierunek (√2/2,√2/2)? to jest ten wektor kierunkowy ktory jest we wzorze na pochodna kierunkowa? vk=(√2/2,√2/2)?

Jerzy: Tak.

dolan: czy moze nalezy pomnozyc 1/1+1 * (√2/2,√2/2) jak tutaj http://blog.etrapez.pl/pochodne/pochodne-kierunkowe-znowu-cos-nowego/

Jerzy: Widzę,że nie czujesz wektora kierunkowego. Jaki będzie wektor kierunkowy pochodnej, dla wektora : [3;1] ?

Jerzy: Właśnie o tym mówię .... tutaj musisz obliczyć wektor kierunkowy ( link) W Twoim zadaniu masz już podany.

dolan:

	1		√x
no to policzylem df/dx =		df/dy = −
	y2√x		y2

podstawiam do wzoru

	1		√2		√x		√2
0=		*		−		*
	y2√x		2		y2		2

dolan: da sie z tego wgl wyliczyc cos?

Adamm: no to wyznacz zależność między x a y

Adamm: da się

Jerzy: I szukaj rozwiązań równania.

Jerzy: x² = 1 ⇔ x = 1 lub x = − 1

Jerzy: Nie ... x = 1

dolan:

	√2		x√2
doszedlem do postaci		=		co teraz?
	4y		2y

dolan: wyszlo mi ze x=1/2 y=R\{0}

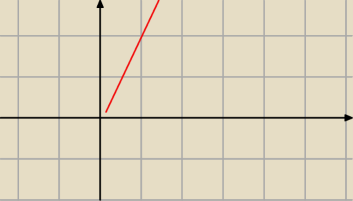
Damian#UDM: y=2x , x>0