pochodną kierunkową funkcji dolan: Obliczyć pochodną kierunkową funkcji f(x, y) = (x²−y)e⁽2y−x) w punkcie (x0,y0)=(1,1) w kierunku wersora tworzącego kąt α = π/3 z dodatnią częścią osi Ox Wiem jak się liczy przy podanym wersorze ale nie wiem jak go dostać z tego opisu

Jerzy: A co dostać ?

dolan: no jak mam polecenie np Obliczyć pochodne kierunkowe podanych funkcji we wskazanych punktach i kierunkach: i jest podane v=(12/13 ,5/13) to licze gradientem a tutaj co mam zrobic

Jerzy: Ponieważ to wersor ( długość 1) więc liczysz tylko jego współrzędne.

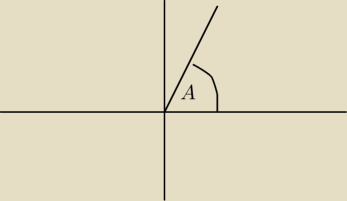
dolan: mam taki rysunek i co dalej?

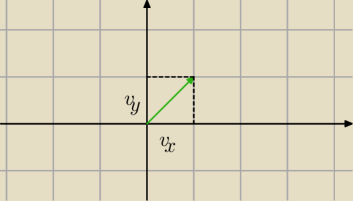
Jerzy: Ponieważ to jest wersor, to ma długość 1 Współrzędne wektora kiewrunkowego liczymy dzieląc jego współrzędne przez jego długość, a skoro tutaj długość podanego wektora ( wersora) wynosi 1, więc wystarczy tylko policzyc jego współrzene i liczyć pochodną w kierunku wktora [v_x,v_y]

dolan: czyli po wyliczeniu df/dx i df/dy , podstawieniu (xo,yo) pod pochodne mnoze grad(1,1) razy (1,1) wynik mi wyszedl e

Jerzy: A jaki masz wektor v ?

dolan: (1,1)? to sie liczy czy nie?

Jerzy: Napisałem Ci wyrażnie, oblicz: v_x i v_y i to będzie Twój wektor kierunkowy.

dolan: nie wiem jak...

Jerzy:

	π
Z funkcji trygonometrycznych kata		( przecież jest podany w treści )
	3

dolan: nie wiem czy to ogarniam biorac np tg π/3 =√3 mam vx=1 i vy=√3?

Jerzy: Ojj .... student/tko

vx		1
	= cos60 =
1		2

vy		√3
	= sin60 =
1		2

	1		√3
vk = [		;		] ... i to jest Twój wektor kierunkowy.
	2		2